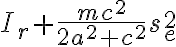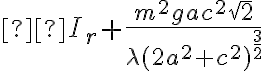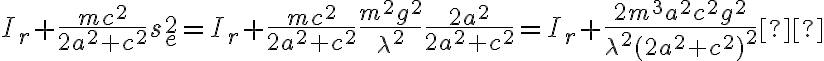Correzione ai Temi d'Esame

Gentile professore,

leggendo la correzione dell’esame scritto del 18-01-21 e provando a svolgerlo per esercizio mi sono accorto che una delle equazioni di Lagrange linearizzate non mi riesca nei calcoli. In particolare l’elemento

$I_r + \dfrac{mc^2}{2a^2+c^2} s_e^2$

nella prima matrice dell’equazione 10.5 diventa, poi, nelle equazioni 10.6

$I_r + \dfrac{m^2 g a c^2 \sqrt{2}}{\lambda (2a^2+c^2)^{\frac{3}{2}}}$

Tuttavia, come trovato nella 5.7, 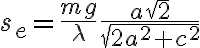$s_e = \frac{mg}{\lambda} \frac{a \sqrt{2}}{\sqrt{2a^2 + c^2}}$. Pertanto, credo che il fattore 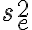$s_e^2$ non sia stato elevato al quadrato, poiché

$I_r + \dfrac{mc^2}{2a^2+c^2} s_e^2 = I_r + \dfrac{mc^2}{2a^2+c^2} \dfrac{m^2 g^2}{\lambda^2} \dfrac{2a^2}{2a^2 + c^2} = I_r + \dfrac{2m^3a^2c^2 g^2}{\lambda^2(2a^2+c^2)^2}$

Le chiedo gentilmente conferma di quanto scritto sopra. La ringrazio anticipatamente e Le porgo cordiali saluti.