Cinematica 1d
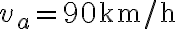 su una strada in cui il limite è
su una strada in cui il limite è 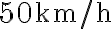 . Una moto della polizia, appostata dietro un cartello pubblicitario, si mette al suo inseguimento partendo 2 secondi dopo che l'auto è passata davanti al cartello. La moto della polizia ha un'accelerazione costante
. Una moto della polizia, appostata dietro un cartello pubblicitario, si mette al suo inseguimento partendo 2 secondi dopo che l'auto è passata davanti al cartello. La moto della polizia ha un'accelerazione costante 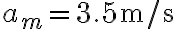
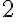 . Dopo quanto tempo la moto raggiunge l'automobile? [SJ E2.8]
. Dopo quanto tempo la moto raggiunge l'automobile? [SJ E2.8]
(B)
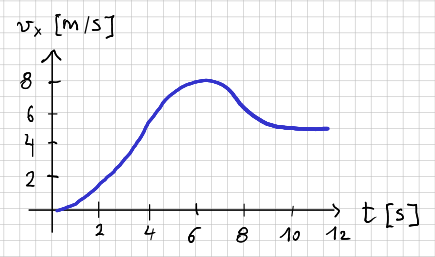
Il diagramma qui sotto mostra la velocità 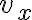 di un'automobile che parte da ferma e si muove lungo una strada rettlinea. (a) Determina l'accelerazione media nell'intervallo di tempo compreso tra
di un'automobile che parte da ferma e si muove lungo una strada rettlinea. (a) Determina l'accelerazione media nell'intervallo di tempo compreso tra 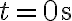 e
e 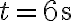 . (b) Stima l'istante in cui l'accelerazione ha il suo massimo valore positivo e il valore dell'accelerazione in quell'istante. (c) Quando si annulla l'accelerazione? (d) In quale istante di tempo l'accelerazione raggiunge il suo massimo valore negativo? [SJ P2.15]
. (b) Stima l'istante in cui l'accelerazione ha il suo massimo valore positivo e il valore dell'accelerazione in quell'istante. (c) Quando si annulla l'accelerazione? (d) In quale istante di tempo l'accelerazione raggiunge il suo massimo valore negativo? [SJ P2.15]
(C) Per misurare la profondità di un pozzo, una studentessa vi lascia cadere una pietra senza velocità iniziale. Dopo misure ripetute, la studentessa stima che il suono della pietra le giunge con un ritardo 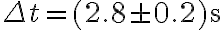 . (a) Trascurando dapprima il tempo di propagazione del suono nell'aria, determina, con il giusto numero di cifre significative, la profondità
. (a) Trascurando dapprima il tempo di propagazione del suono nell'aria, determina, con il giusto numero di cifre significative, la profondità 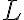 del pozzo. (b) Stima in modo semplice l'errore introdotto nella misura della profondità del pozzo se si trascura il tempo di propagazione del suono. La velocità del suono nell'aria è
del pozzo. (b) Stima in modo semplice l'errore introdotto nella misura della profondità del pozzo se si trascura il tempo di propagazione del suono. La velocità del suono nell'aria è 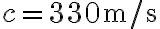 . (c) Determina
. (c) Determina 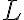 in funzione di
in funzione di 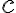 ,
, 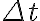 e
e 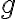 e riconsidera la stima ottenuta al punto (b). [SJ P2.49]
e riconsidera la stima ottenuta al punto (b). [SJ P2.49]
Cinematica 2d
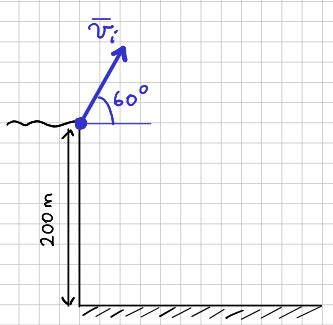
(A) Un proiettile è sparato nell'aria dalla cima di una rupe alta 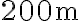 . Il modulo della velocità iniziale del proiettile è
. Il modulo della velocità iniziale del proiettile è 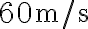 , l'angolo formato tra la velocità iniziale e l'orizzontale è
, l'angolo formato tra la velocità iniziale e l'orizzontale è 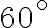 . Trascurando la resistenza dell'aria, in quale punto il proiettile colpisce il suolo? Per quanto tempo resta in aria?
. Trascurando la resistenza dell'aria, in quale punto il proiettile colpisce il suolo? Per quanto tempo resta in aria?
(B) Una ragazza fa roteare una palla attaccata ad una corda facendole descrivere una traiettoria circolare di 1 m di raggio su un piano parallelo all'orizzontale. Supponendo che la velocità della palla sia costante in modulo, quanti giri al minuto deve compiere la palla affinchè la sua accelerazione centripeta abbia lo stesso valore dell'accelerazione di gravità?
