Dinamica
Ordini di grandezza
(A) Stima la differenza relativa tra l'accelerazione di gravità terrestre all'equatore e quella ai poli.
(B) Stima l'ordine di grandezza della forza d'attrazione gravitazionale tra due persone.
Equilibrio statico
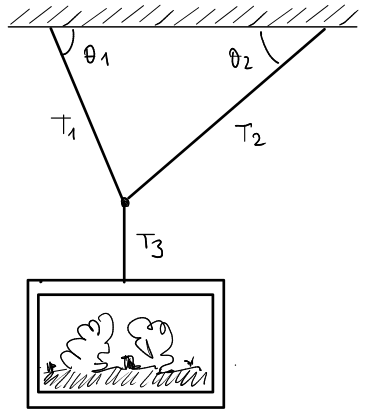
(A) Un quadro di peso 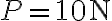 è mantenuto in equilibrio statico da tre funi come mostrato in figura. Le funi formano gli angoli
è mantenuto in equilibrio statico da tre funi come mostrato in figura. Le funi formano gli angoli 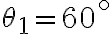 e
e 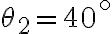 con l'orizzontale. Trova le tensioni
con l'orizzontale. Trova le tensioni 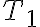 ,
, 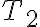 e
e 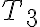 in ciascuna delle funi.
in ciascuna delle funi.
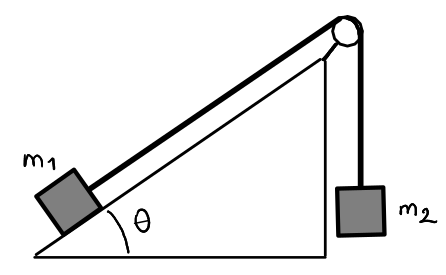
(B) Un corpo di massa 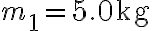 su un piano inclinato di
su un piano inclinato di 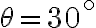 è attaccato a un filo che scorre senza attrito su un piolo liscio e alla cui altra estremità è attaccato un secondo corpo di massa
è attaccato a un filo che scorre senza attrito su un piolo liscio e alla cui altra estremità è attaccato un secondo corpo di massa 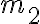 . Il coefficiente di attrito statico tra il primo corpo e il piano inclinato è
. Il coefficiente di attrito statico tra il primo corpo e il piano inclinato è 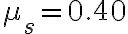 . (a) Trova l'intervallo di valori di
. (a) Trova l'intervallo di valori di 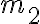 tali che i due corpi siano in equilibrio statico. (b) Se
tali che i due corpi siano in equilibrio statico. (b) Se 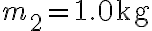 i due corpi sono in equilibrio statico. Qual è la forza di attrito statico sul corpo di massa
i due corpi sono in equilibrio statico. Qual è la forza di attrito statico sul corpo di massa 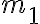 ?
?
(C) Due molle hanno rispettivamente costanti elastiche 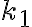 e
e 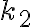 e lunghezze a riposo identiche
e lunghezze a riposo identiche 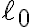 .
.
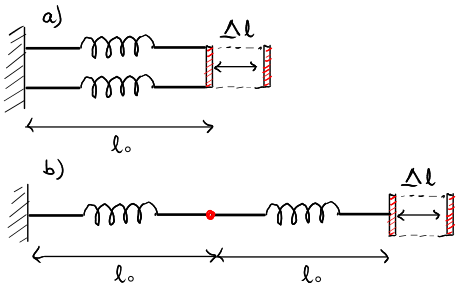
(a) Le molle sono dapprima disposte "in parallelo" come mostrato in figura a). La barretta verticale a cui sono agganciate le estremità libere delle molle potrà essere assimilata a un punto. Ciascuna molla si allunga di 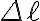 . Mostra che il modulo della forza misurata all'estremità libera della molla si può scrivere nella forma
. Mostra che il modulo della forza misurata all'estremità libera della molla si può scrivere nella forma 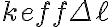 e trova l'espressione di
e trova l'espressione di 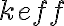 .
.
(b) Le molle sono ora disposte "in serie" come mostrato in figura b). L'allungamento complessivo delle due molle è 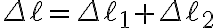 . Mostra che il modulo della forza misurata all'estremità libera della molla si può scrivere nella forma
. Mostra che il modulo della forza misurata all'estremità libera della molla si può scrivere nella forma 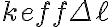 e trova l'espressione di
e trova l'espressione di 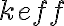 .
.
Equazioni del moto
(A) Tre blocchi, rispettivamente di massa 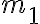 ,
, 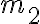 e
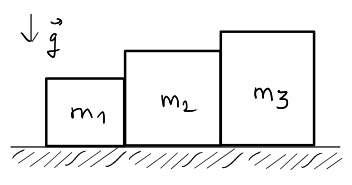
e 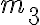 , sono in contatto l'uno contro l'altro su una superficie orizzontale priva di attrito. Applichi una forza
, sono in contatto l'uno contro l'altro su una superficie orizzontale priva di attrito. Applichi una forza 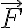 diretta lungo l'orizzontale contro il blocco di massa
diretta lungo l'orizzontale contro il blocco di massa 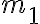 . Trova l'accelerazione dei blocchi, la forza risultante su ciascuno dei blocchi e i moduli delle forze di reazione tra i blocchi. Applicazione numerica:
. Trova l'accelerazione dei blocchi, la forza risultante su ciascuno dei blocchi e i moduli delle forze di reazione tra i blocchi. Applicazione numerica: 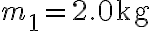 ,
, 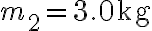 ,
, 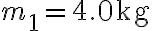 ,
, 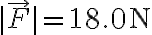 .[SJ P4.49]
.[SJ P4.49]
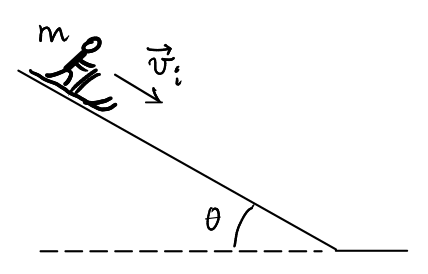
(B) Una sciatrice si lascia scivolare lungo una pista da sci di lunghezza 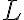 partendo con una velocità iniziale di modulo
partendo con una velocità iniziale di modulo 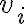 . La pendenza della pista rispetto all'orizzontale è
. La pendenza della pista rispetto all'orizzontale è 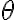 . Il coefficiente di attrito dinamico tra gli sci e la neve della pista è
. Il coefficiente di attrito dinamico tra gli sci e la neve della pista è 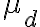 . (a) Determina le leggi orarie del moto della sciatrice. (b) Determina la pendenza minima
. (a) Determina le leggi orarie del moto della sciatrice. (b) Determina la pendenza minima 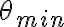 affinchè la sciatrice arrivi in fondo alla pista. (c) Determina, nell'ipotesi che
affinchè la sciatrice arrivi in fondo alla pista. (c) Determina, nell'ipotesi che 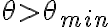 il tempo che impiegherà ad arrivare in fondo alla pista.
il tempo che impiegherà ad arrivare in fondo alla pista.
(C) Una piccola palla di massa 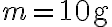 è sospesa a un filo di lunghezza
è sospesa a un filo di lunghezza 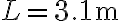 . La palla ruota percorrendo una traiettoria circolare di raggio
. La palla ruota percorrendo una traiettoria circolare di raggio 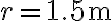 con velocità di modulo costante, in modo che il filo descrive la superficie di un cono ("pendolo conico"). Trova il modulo della velocità della palla e la tensione del filo. [SJ E5.5]
con velocità di modulo costante, in modo che il filo descrive la superficie di un cono ("pendolo conico"). Trova il modulo della velocità della palla e la tensione del filo. [SJ E5.5]
