Energia e quantità di moto
Domande concettuali
(A) (a) Il lavoro 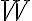 compiuto dalla risultante
compiuto dalla risultante  delle forze agenti su un corpo può essere negativo? Perchè? (b) Il valore assoluto
delle forze agenti su un corpo può essere negativo? Perchè? (b) Il valore assoluto 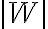 del lavoro compiuto da
del lavoro compiuto da  può essere maggiore dell'energia cinetica iniziale del corpo? Perchè?
può essere maggiore dell'energia cinetica iniziale del corpo? Perchè?
(B) Per ciascuna delle affermazioni seguenti dire se è vera o falsa, spiegando perchè:
- (a) solo le forze conservative compiono lavoro
- (b) se su corpo agiscono solo forze conservative, la sua energia cinetica non cambia
- (c) l'energia meccanica di un corpo deve essere maggiore o uguale a zero
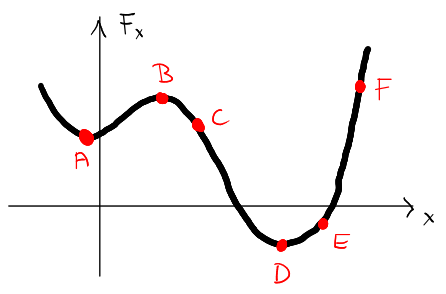
(C) La figura mostra l'energia potenziale 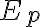 di un corpo in funzione della sua posizione
di un corpo in funzione della sua posizione 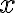 . (a) In ogni punto indicato in figura, dire se la forza
. (a) In ogni punto indicato in figura, dire se la forza 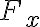 è positiva, negativa, o nulla. (b) In quale di questi punti la forza ha il modulo maggiore? (c) Trova gli eventuali punti di equilibrio indicando se sono stabili o instabili.
è positiva, negativa, o nulla. (b) In quale di questi punti la forza ha il modulo maggiore? (c) Trova gli eventuali punti di equilibrio indicando se sono stabili o instabili.
Energia potenziale
(A) Trova l'energia potenziale 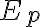 associata ad un corpo su cui agisce una forza costante
associata ad un corpo su cui agisce una forza costante 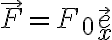 , dove
, dove 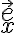 è il versore orientato come l'asse x, in modo tale che
è il versore orientato come l'asse x, in modo tale che 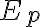 sia nulla nel punto $x=0$ m. Ridefinisci quindi l'energia potenziale in modo che sia nulla nel punto $x=10$ m. Perchè questa modifica non altera il comportamento dei corpi soggetti alla forza
sia nulla nel punto $x=0$ m. Ridefinisci quindi l'energia potenziale in modo che sia nulla nel punto $x=10$ m. Perchè questa modifica non altera il comportamento dei corpi soggetti alla forza 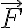 ?
?
(B) Una molla segue la legge di Hooke con una costante elastica 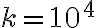 N/m. Di quanto deve essere allungata perchè la sua energia potenziale sia 50 J?
N/m. Di quanto deve essere allungata perchè la sua energia potenziale sia 50 J?
(C) Una massa 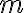 si trova a una distanza
si trova a una distanza 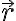 da un'altra massa
da un'altra massa 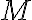 posta all'origine del sistema di coordinate. (a) Quale è il lavoro compiuto dalla forza gravitazionale
posta all'origine del sistema di coordinate. (a) Quale è il lavoro compiuto dalla forza gravitazionale 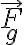 sulla massa
sulla massa 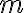 se la massa
se la massa 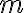 si sposta dalla posizione
si sposta dalla posizione 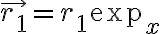 a
a 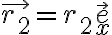 lungo l'asse
lungo l'asse 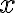 , e la massa
, e la massa 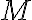 resta immobile? (b) Sappiamo che il lavoro compiuto da
resta immobile? (b) Sappiamo che il lavoro compiuto da 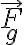 su
su 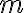 non dipende dal percorso. Sfrutta il risultato ottenuto al punto (a) per trovare l'espressione dell'energia potenziale gravitazionale
non dipende dal percorso. Sfrutta il risultato ottenuto al punto (a) per trovare l'espressione dell'energia potenziale gravitazionale 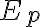 in funzione della distanza
in funzione della distanza 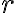 dall'origine, in modo tale che
dall'origine, in modo tale che 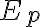 si annulli quando
si annulli quando 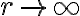 .
.
Conservazione dell'energia
(A) Una palla di 0.2 kg è lanciata con una velocità iniziale di modulo 24 m/s e con un angolo 53 rispetto all'orizzontale. L'accelerazione di gravità vale $g=9.81$ m/s. Trascura la resistenza dell'aria e sfrutta la conservazione dell'energia per determinare l'altezza massima raggiunta dalla palla.
rispetto all'orizzontale. L'accelerazione di gravità vale $g=9.81$ m/s. Trascura la resistenza dell'aria e sfrutta la conservazione dell'energia per determinare l'altezza massima raggiunta dalla palla.
(B) Un blocco di massa $m=10$ kg è lasciato libero da un'altezza $h=3$ m ( punto A indicato in figura). L'accelerazione di gravità vale $g=9.81$ m/s. La pista è priva di attrito all'eccezione del tratto compreso tra i punti B e C, lungo 6 m. Il blocco scende lungo la guida colpisce una molla di costante elastica $k=2250$ N/m e ne determina una compressione massima di 0.3 m rispetto alla sua lunghezza a riposo. Determina il coefficiente di attrito dinamico tra il blocco e la superficie della pista nel tratto compreso tra B e C. [SJ 7.71]
(C) Un pendolo, composto da una piccola sfera di massa 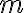 appesa a un filo di massa trascurabile e di lunghezza
appesa a un filo di massa trascurabile e di lunghezza 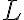 , oscilla lungo un piano verticale. L'accelerazione di gravità è $g=9.81$ m/s^2. Il filo urta contro un piolo, posizionato a una distanza
, oscilla lungo un piano verticale. L'accelerazione di gravità è $g=9.81$ m/s^2. Il filo urta contro un piolo, posizionato a una distanza 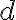 sotto il punto a cui è sospeso il pendolo, e si avvoolge attorno ad esso. (a) Mostra che se
sotto il punto a cui è sospeso il pendolo, e si avvoolge attorno ad esso. (a) Mostra che se 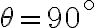 , l'altezza massima raggiunta dalla sfera è uguale a quella iniziale. (b) Mostra che se il pendolo è rilasciato da fermo dalla posizione orizzontale (
, l'altezza massima raggiunta dalla sfera è uguale a quella iniziale. (b) Mostra che se il pendolo è rilasciato da fermo dalla posizione orizzontale (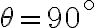 ) e vogliamo che oscilli compiendo un giro completo attorno al piolo, il valore minimo di
) e vogliamo che oscilli compiendo un giro completo attorno al piolo, il valore minimo di 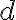 deve essere
deve essere 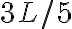 .
.

Quantità di moto
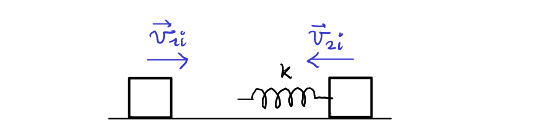
(A) Un blocco di massa $m_1=1.6$ kg, inizialmente in moto con una velocità di $4$ m/s verso destra su un piano orizzontale privo di attrito, urta con una molla di massa trascurabile agganciata a un secondo blocco di massa $m_2=2.1$ kg, in moto verso sinistra ad una velocità di 2.5 m/s. La costante elastica della molla è 600 N/m. (a) Determina le velocità dei due blocchi dopo l'urto. (b) Di che tipo di urto si tratta? Perchè? (c) Determina la velocità del blocco 2 durante la collisione nell'istante in cui il blocco 1 si muove verso destra con velocità 3.0 m/s. [SJ E8.8]
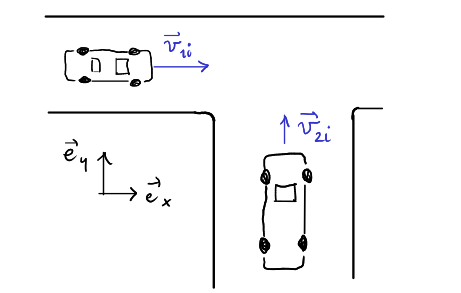
(B) Un'automobile di 1500 kg che viaggia verso est a una velocità di 25 m/s urta a un incrocio con un furgone di 2500 kg che viaggia verso nord a 20 m/s. Calcola la direzione e il modulo della velocità dei rottami dopo l'urto, assumendo che questo sia perfettamente anelastico (cioè che i veicoli restino incastrati) [SJ E8.10]