Oscillazioni
Moto armonico
(A) Una particelle di massa 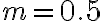 kg è attaccata a una molla ideale di costante elastica
kg è attaccata a una molla ideale di costante elastica 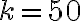 N/m e disposta orizzontalmente. Sul sistema molla+massa non agiscono forze esterne. All'istante
N/m e disposta orizzontalmente. Sul sistema molla+massa non agiscono forze esterne. All'istante 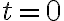 , la particella ha una velocità massima di 20 m/s e si muove verso sinistra. (a) Trova l'equazione del moto della particella, specificando la sua posizione in funzione del tempo. (b) In quale stato l'energia potenziale è 3 volte l'energia cinetica della massa? (c) Trova l'intervallo di tempo minimo necessario alla particella per muoversi da
, la particella ha una velocità massima di 20 m/s e si muove verso sinistra. (a) Trova l'equazione del moto della particella, specificando la sua posizione in funzione del tempo. (b) In quale stato l'energia potenziale è 3 volte l'energia cinetica della massa? (c) Trova l'intervallo di tempo minimo necessario alla particella per muoversi da 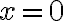 and
and 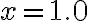 . [SJ 12.51]
. [SJ 12.51]
(B) L'interazione tra due atomi neutri può essere descritta tramite l'energia potenziale di Lennard-Jones
![E_p(r) = 4\epsilon [(\sigma/r)^{12} - (\sigma/r)^{6}]
E_p(r) = 4\epsilon [(\sigma/r)^{12} - (\sigma/r)^{6}]](https://moodle2.units.it/filter/tex/pix.php/54430336b4e29e9b98044e26acc57043.gif) dove
dove 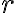 è la distanza tra gli atomi,
è la distanza tra gli atomi, 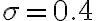 nm e
nm e 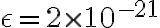 J. (a) Trova la distanza
J. (a) Trova la distanza 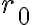 di equilibrio dei due atomi. (b) Supponendo che gli atomi restino vicini alla configurazione di equilibrio e che la massa oscillante sia
di equilibrio dei due atomi. (b) Supponendo che gli atomi restino vicini alla configurazione di equilibrio e che la massa oscillante sia 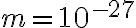 kg, determina il periodo delle oscillazioni attorno a
kg, determina il periodo delle oscillazioni attorno a 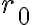 .
.
Pendolo semplice
(A) Un pendolo semplice di lunghezza 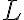 è lasciato oscillare a partire da un angolo
è lasciato oscillare a partire da un angolo 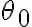 rispetto alla verticale, senza velocità iniziale. (a) Supponendo che
rispetto alla verticale, senza velocità iniziale. (a) Supponendo che 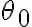 sia tale che
sia tale che 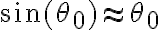 , trova il modulo
, trova il modulo 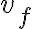 della velocità del pendolo quando passa per
della velocità del pendolo quando passa per 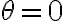 . (b) Usando la conservazione dell'energia meccanica, trova
. (b) Usando la conservazione dell'energia meccanica, trova 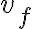 esattamente. (c) Calcola la differenza tra i due risultati per
esattamente. (c) Calcola la differenza tra i due risultati per 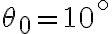 e
e 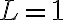 m.
m.
