Meccanica dei fluidi
Fluidostatica
(A) Il titanic riposa a 4000 m di profondità sotto il livello del mare. Supponendo che l'acqua si comporti come un liquido incomprimibile di densità 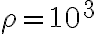
 , quale pressione esercita sul titanic?
, quale pressione esercita sul titanic?
(B) Un palloncino sferico riempito di elio, di raggio 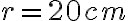 e di massa complessiva
e di massa complessiva 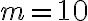 g, sfugge di mano a un bambino ed è lasciato libero nell'atmosfera. Supponi che l'aria possa essere descritta come un gas perfetto di massa molare
g, sfugge di mano a un bambino ed è lasciato libero nell'atmosfera. Supponi che l'aria possa essere descritta come un gas perfetto di massa molare 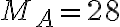 g/mol e che la pressione vari con l'altitudine
g/mol e che la pressione vari con l'altitudine 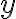 secondo la legge
secondo la legge
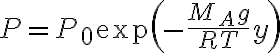 con
con 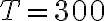 K e
K e 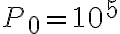 Pa. Trova, nell'ipotesi di atmosfera statica e isoterma, a quale altitudine il palloncino sarà in equilibrio statico. L'equilibrio è stabile, instabile o indifferente? Perchè? Nota: potrai trascurare la variazione di densità dell'atmosfera su una scala di lunghezze inferiore a
Pa. Trova, nell'ipotesi di atmosfera statica e isoterma, a quale altitudine il palloncino sarà in equilibrio statico. L'equilibrio è stabile, instabile o indifferente? Perchè? Nota: potrai trascurare la variazione di densità dell'atmosfera su una scala di lunghezze inferiore a 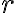 .
.
(C) Nella fascia di atmosfera più vicina alla superficie terrestre, detta troposfera, la temperatura decresce linearmente in funzione dell'altitudine
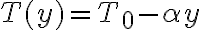 dove
dove 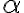 è una costante positiva chiamata "gradiente termico". Supponendo che il gas presente nell'atmosfera si comporti come un gas perfetto di massa molare
è una costante positiva chiamata "gradiente termico". Supponendo che il gas presente nell'atmosfera si comporti come un gas perfetto di massa molare 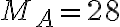 g/mol, mostra che la variazione della pressione
g/mol, mostra che la variazione della pressione 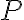 in funzione dell'altitudine
in funzione dell'altitudine 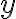 si può scrivere
si può scrivere
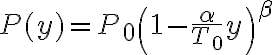 dove
dove 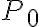 è la pressione a livello della superficie terrestre e
è la pressione a livello della superficie terrestre e 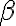 una grandezza adimensionale. Qual è l'espressione di
una grandezza adimensionale. Qual è l'espressione di 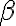 e quanto vale? Qual è la pressione a un'altitudine di 10 km se
e quanto vale? Qual è la pressione a un'altitudine di 10 km se 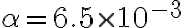 K/m,
K/m, 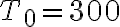 K e
K e 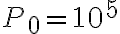 Pa?
Pa?
Fluidodinamica
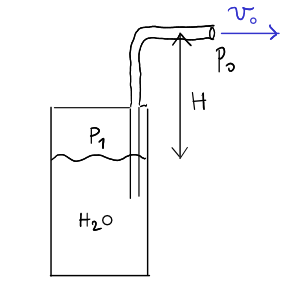
(A) L'acqua in un estintore costretta a uscire è forzata ad uscire dalla pressione 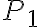 di una gas contenuto nella parte alta dell'estintore stesso. Il livello di uscita dell'acqua è di 50 cm superiore alla superficie dell'acqua all'interno nell'estintore. Al livello di uscita, l'acqua è alla pressione atmosferica
di una gas contenuto nella parte alta dell'estintore stesso. Il livello di uscita dell'acqua è di 50 cm superiore alla superficie dell'acqua all'interno nell'estintore. Al livello di uscita, l'acqua è alla pressione atmosferica 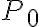 . Determina la differenza di pressione
. Determina la differenza di pressione 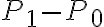 affinchè la velocità di uscita dell'acqua sia 30 m/s. Di quanto deve essere superiore a
affinchè la velocità di uscita dell'acqua sia 30 m/s. Di quanto deve essere superiore a 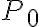 ? [SJ 15.53]
? [SJ 15.53]
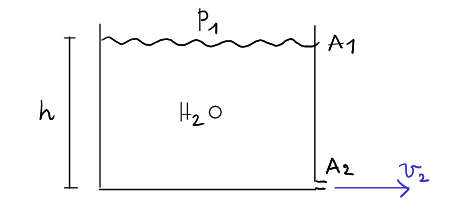
(B) Un barile di altezza 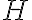 e area
e area 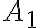 è colmo di acqua. La parte superiore è aperta ed è esposta alla pressione atmosferica
è colmo di acqua. La parte superiore è aperta ed è esposta alla pressione atmosferica 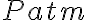 . Sul fondo del barile c'è un'apertura di area
. Sul fondo del barile c'è un'apertura di area 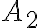 , molto più piccola di
, molto più piccola di 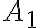 . (a) Mostra che la velocità di uscita dell'acqua è circa
. (a) Mostra che la velocità di uscita dell'acqua è circa 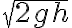 quando l'altezza dell'acqua è
quando l'altezza dell'acqua è 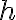 . (b) Mostra che se
. (b) Mostra che se 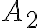 , la rapidità di variazione dell'altezza
, la rapidità di variazione dell'altezza 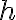 è data da
è data da
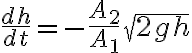 .
(c) Integra l'equazione per separazione delle variabili, assumendo che all'istante t=0, h=H. (d) Determina il tempo necessario a svuotare il barile se
.
(c) Integra l'equazione per separazione delle variabili, assumendo che all'istante t=0, h=H. (d) Determina il tempo necessario a svuotare il barile se 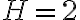 m,
m, 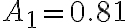 m
m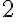 e
e 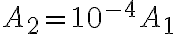 .
.