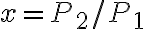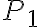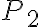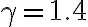Secondo principio
(A) Variazioni di entropia in processi irreversibili
Un oggetto metallico di capacità termica 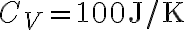 viene estratto da una fornace a
viene estratto da una fornace a 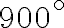 e immerso in un ampio bacino d'acqua a
e immerso in un ampio bacino d'acqua a 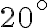 . Supponendo che il bacino d'acqua si comporti come un termostato di temperatura costante e che non ci si scambio di calore del sistema {oggetto, bacino} con l'ambiente esterno, determina la variazione di entropia dell'oggetto, del bacino e del sistema {oggetto, bacino}. La trasformazione è reversibile o irreversibile? Perchè?
. Supponendo che il bacino d'acqua si comporti come un termostato di temperatura costante e che non ci si scambio di calore del sistema {oggetto, bacino} con l'ambiente esterno, determina la variazione di entropia dell'oggetto, del bacino e del sistema {oggetto, bacino}. La trasformazione è reversibile o irreversibile? Perchè?
Supponiamo ora che il bacino d'acqua, invece di essere un termostato, abbia una capacità termica finita, pari a 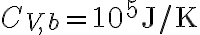 . Supponendo che l'oggetto e il bacino d'acqua abbiano le stesse temperature iniziali considerate nella prima parte dell'esercizio, qual'è la temperatura finale di equilibrio del sistema {oggetto, bacino}? Determina nuovamente la variazione di entropia dell'oggetto, del bacino e del sistema {oggetto, bacino}.
. Supponendo che l'oggetto e il bacino d'acqua abbiano le stesse temperature iniziali considerate nella prima parte dell'esercizio, qual'è la temperatura finale di equilibrio del sistema {oggetto, bacino}? Determina nuovamente la variazione di entropia dell'oggetto, del bacino e del sistema {oggetto, bacino}.
(B) Variazione di entropia in una transizione di fase
Un litro di acqua in fase liquida, inizialmente a una temperatura di 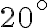 , viene riscaldato quasi-staticamente a pressione atmosferica costante fino a raggiungere
, viene riscaldato quasi-staticamente a pressione atmosferica costante fino a raggiungere 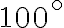 . Sapendo che la capacità termica dell'acqua a pressione costante è
. Sapendo che la capacità termica dell'acqua a pressione costante è 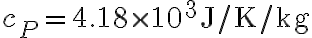 e che la sua densità è
e che la sua densità è 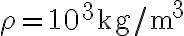 , calcola la variazione di entropia dell'acqua.
, calcola la variazione di entropia dell'acqua.
L'acqua viene successivamente fatta evaporare e si trasforma completamente in vapore a una temperatura di 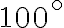 . Calcola la variazione di entropia dell'acqua durante l'evaporazione, sapendo che il calore latente di evaporazione a pressione atmosferica vale
. Calcola la variazione di entropia dell'acqua durante l'evaporazione, sapendo che il calore latente di evaporazione a pressione atmosferica vale 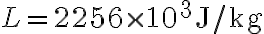 . Commenta il risultato.
. Commenta il risultato.
(C) Ciclo di Carnot per un gas perfetto
Consideriamo una mole di gas perfetto che effettua un ciclo di Carnot composto dalle seguenti trasformazioni reversibili
La temperatura del gas nello stato 1 è 410 K, le pressioni negli stati 1, 2 e 3 sono rispettivamente 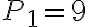 bar,
bar, 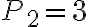 bar e
bar e 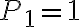 bar. Il parametro
bar. Il parametro 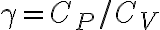 vale 7/5.
vale 7/5.
- Traccia il ciclo nel diagramma
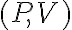
- Traccia il ciclo nel diagramma
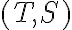
- Determina il lavoro e il calore scambiato dal gas durante ciascuna delle trasformazioni. Il ciclo corrisponde a un motore termico o a un frigorifero?
- Determina l'efficienza del ciclo e calcola il sua valore numerico.
- Determina la variazione di entropia del gas associata a ciascuna delle trasformazioni e quindi la variazione totale di entropia del gas dopo un ciclo. Commenta il risultato.
(D) Ordini di grandezza
In questo esercizio modellizziamo il corpo umano come una motore termico di Carnot che funziona tra un termostato caldo a temperatura 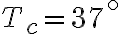 (temperatura corporea) e un termostato freddo a
(temperatura corporea) e un termostato freddo a 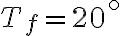 (temperatura ambiente). Stima l'ordine di grandezza del calore ceduto per unità di tempo dal tuo corpo all'ambiente esterno.
(temperatura ambiente). Stima l'ordine di grandezza del calore ceduto per unità di tempo dal tuo corpo all'ambiente esterno.
(E) Frigorifero
Un frigorifero di efficienza 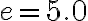 assorbe una potenza media pari a
assorbe una potenza media pari a 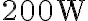 , che utilizza integralmente per produrre il lavoro meccanico necessario al suo funzionamento (ovvero la compressione del fluido refrigerante durante una delle trasformazioni del ciclo). Calcola il calore ceduto all'ambiente esterno (ovvero la cucina) durante 8 ore di funzionamento continuo del frigorifero.
, che utilizza integralmente per produrre il lavoro meccanico necessario al suo funzionamento (ovvero la compressione del fluido refrigerante durante una delle trasformazioni del ciclo). Calcola il calore ceduto all'ambiente esterno (ovvero la cucina) durante 8 ore di funzionamento continuo del frigorifero.
(F) Ciclo di Lenoir
Il primo motore a combustione interna a due tempi funzionava secondo il ciclo di Lenoir, descritto schematicamente dalle seguenti trasformazioni quasi-statiche:
- 1
 2: combustione della miscela di aria e carburante a volume costante
2: combustione della miscela di aria e carburante a volume costante - 2
 3: espansione adiabatica
3: espansione adiabatica - 3
 1: raffreddamento a pressione costante
1: raffreddamento a pressione costante
Il modello utilizzato in questo esercizio corrisponde a un ciclo di un sistema chiuso, in cui la miscela di aria e carburante è descritta come un gas perfetto di costante 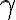 .
.