Point Symmetry in Crystals and Molecular Structures
CRYSTALLINE STRUCTURES
The Crystalline State
A condensed phase in which matter is arranged with periodic translational symmetry.
In addition to the translational symmetry of the crystal lattice, other symmetry operators that relate the molecules to each other are also present.
This means that the chemical entities within the crystal are interconnected by symmetry elements that repeat consistently and periodically in three-dimensional space.
To understand the periodic and orderly arrangement of atoms and molecules in crystals, it is first necessary to introduce the characteristics and properties of symmetry elements and their corresponding symmetry operations, through which the fundamental structural motif (asymmetric unit) generates the entire crystalline structure by regular repetition.
Symmetry Element
A geometric entity (point, axis, or plane) with respect to which a given symmetry operation is performed

Symmetry Operation
A movement that transforms an object (molecule) into an identical or equivalent object to the original one (a congruent object: same shape and dimensions; same bond lengths and angles).
Congruence
Direct (same torsional angles); Indirect (torsional angles with opposite signs)


Rotations Inversions and Reflections
Symmetry axes Symmetry points and planes
If the symmetry operation leaves at least one point unchanged, it is called point symmetry.
Point symmetry in three-dimensional space.
Identity
All objects (molecules) have at least the identity element.
The point with coordinates x, y, z has as its symmetric equivalent the same point with coordinates x, y, z.
In matrix terms:
|x’| |1 0 0| |x|
|y’| = |0 1 0| |y|
|z’| |0 0 1| |z|
The identity symmetry element is denoted by:
E or C1 in the Schoenflies notation, is primarily used to describe the point group symmetry of molecules and is commonly used for spectroscopy.
1 in the Hermann-Mauguin notation, is primarily used to describe the space group symmetry of crystals and is commonly used for crystallography.
It is equivalent to a 360° rotation around an axis (axis of order 1).
Many chiral molecules have only the identity element E (from the German Einheit, meaning unit).
For example, leucine and codified amino acids, excluding glycine (point group C1).
Some molecules crystallize in the triclinic crystal system and have, in addition to the identity, only the translation operations of the unit cell as their crystal symmetry (space group P1)
Note that even centrosymmetric molecules can crystallize in non-centrosymmetric space groups, as seen in the example of N,N,N',N'-tetramethyl-N,N'-dipropyl-ethylenediammonium chloride.
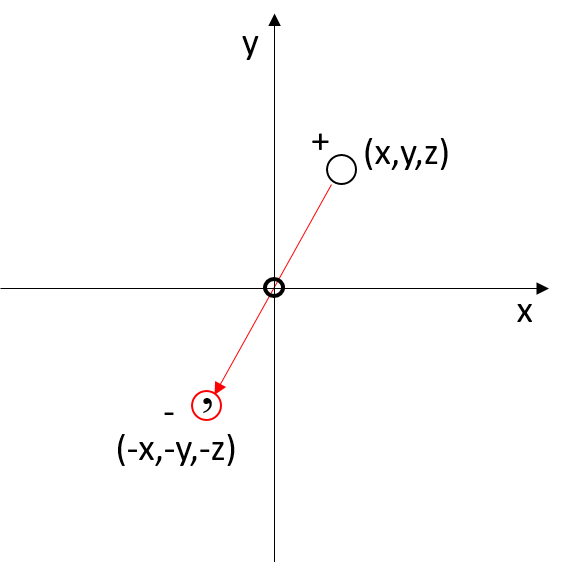
Inversion Center
The symmetry element is a point, and the operation involves inverting the coordinates.
If the inversion center is placed at the origin, the point with coordinates x, y, z has as its symmetric equivalent the point with coordinates -x, -y, -z.
In matrix terms:
|x’| |-1 0 0| |x|
|y’| = | 0 -1 0| |y|
|z’| | 0 0 -1| |z|
Applying the inversion center twice results in the identity.
|x’| |-1 0 0| |-1 0 0||x| |1 0 0||x|
|y’| = | 0 -1 0| | 0 -1 0||y| = |0 1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| |0 0 1||z|
The symmetry element inversion center is denoted by:
i (inversion) in the Schoenflies notation
 in the Hermann-Mauguin notation
in the Hermann-Mauguin notation
It is equivalent to an axis of order 1 (360° rotation) with inversion (bar) (improper axis of rotoinversion of order 1).
The graphical symbol used for the inversion point in the International Tables for Crystallography is:
°
A molecule that possesses an inversion center is a centrosymmetric molecule.
For example, the meso form of tartaric acid (point group Ci).
Two molecules related by an inversion center exhibit indirect congruence (enantiomorphous). If they are chiral molecules, they are non-superimposable and form an enantiomeric pair.
Centrosymmetric crystals (those with inversion centers) of chiral molecules consist of a racemic mixture of the compound.
For example, a racemic mixture of a chiral molecule that crystallizes with a centrosymmetric triclinic unit cell (space group P ).
).
While triclinic symmetry P1 is compatible with all molecules, triclinic symmetry P is incompatible with enantiopure chiral molecules.
is incompatible with enantiopure chiral molecules.
Symmetry Axes (Proper Type) of Order n
The symmetry element is an axis, and the symmetry operation is a rotation around the axis by 360°/n, where n indicates the order of the rotation.
A molecule possesses a given symmetry element if all the symmetry operations associated with that element are verified.
For example, a molecule has a rotation axis of order n if all n rotations of 360°/n result in n superpositions of the original molecule.
The symmetry element of a proper rotation axis of order n is denoted by:
Cn (Cyclic) in the Schoenflies notation
n in the Hermann-Mauguin notation
A specific m symmetry operation around an axis of order n is denoted with a superscript m, Cnm, which indicates the amount of rotation to apply: equal to m × 360°/n. When m = n, a complete rotation is performed, equivalent to the identity operation E.
Proper rotation axes are compatible with chiral molecules, and in crystals, these symmetry operators relate molecules with the same chirality (congruent objects in a direct manner).
Proper rotation axes are the only point symmetry elements compatible with chiral systems.
Molecules that have only proper rotation axes of order >1 as their symmetry are called dissymmetric.
Chiral molecules can be asymmetric (with only proper rotation axes of order 1) or dissymmetric (with only proper rotation axes of order >1).
Rotation Axes Compatible with Crystal Lattices
Not all rotation axes are compatible with the translational symmetry of the crystal lattice.
A symmetry element is an integral part of the crystal symmetry if and only if it is compatible with the periodic symmetry of the crystal lattice.
Considering that the choice of origin is arbitrary, if the origin is placed on a symmetry element, all lattice points will contain this symmetry element. This implies that lattice points must also be related to each other by these symmetry elements.
Analyzing the problem of tiling in two-dimensional space, we can easily determine which symmetry axes are compatible with a crystal lattice.
Twofold axis

Twofold axis (proper axis of order 2) = rotation of 360/2 = 180°
If the rotation axis is along the y-axis, the point with coordinates (x,y,z) has its symmetry-equivalent point at (−x,y,−z).
In matrix form, a 180° rotation about the y-axis is represented by the following rotation matrix:
|x’| |-1 0 0| |x|
|y’| = | 0 1 0| |y|
|z’| | 0 0 -1| |z|
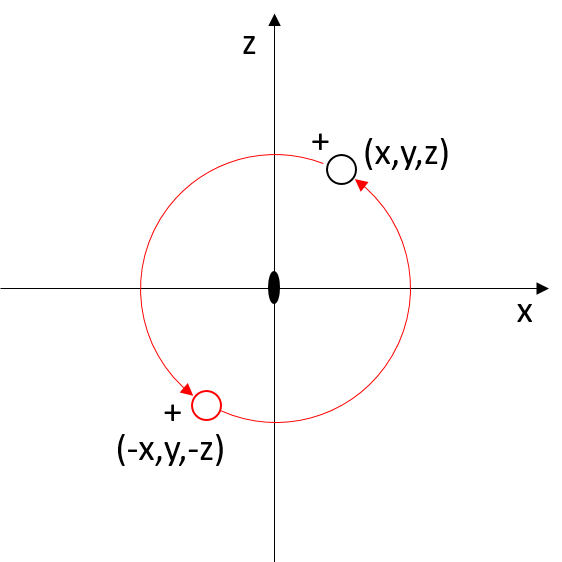
Applying the twofold rotation twice results in the identity transformation.
C21C21 = C22 = E
|x’| |-1 0 0| |-1 0 0||x| |1 0 0||x|
|y’| = | 0 1 0| | 0 1 0||y| = |0 1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| |0 0 1||z|
Symbols used in the description of symmetry in the International Tables for Crystallography
for 2-fold axis
Orthogonal, Parallel and Diagonal to the sheet plane:

Chiral molecules can also have symmetry axes
E.g., (R,R)-2,5-dimethylpyrrolidine is a chiral symmetric molecule (point group C₂).
Proper symmetry axes, translations, and their combinations (such as roto-translation axes) are the only symmetry operations in crystals compatible with any molecule, including enantiopure chiral molecules.
Threefold axis

Threefold axis (proper axis of order 3) = rotations of 360/3 = 120°
If the rotation axis is along the z-axis and a hexagonal coordinate system is used (with the angle γ between the x and y axes = 120°), the point with coordinates x,y,z has as its first symmetry-equivalent point the point with coordinates −y,x−y,z.
In matrix form, a 120° rotation around the z-axis in a hexagonal system can be represented by the following matrix:
|x’| | 0 -1 0| |x|
|y’| = | 1 -1 0| |y|
|z’| | 0 0 1| |z|
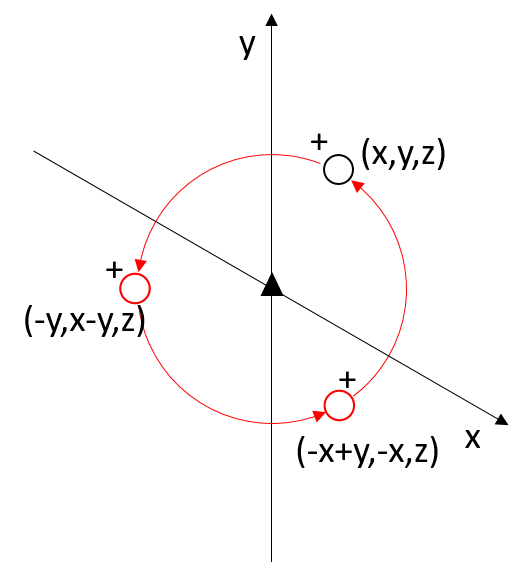
Applying the threefold rotation twice generates a second symmetry-equivalent point with coordinates −x+y,−x,z.
C31C31 = C32
|x’| | 0 -1 0| | 0 -1 0||x| |-1 1 0||x|
|y’| = | 1 -1 0| | 1 -1 0||y| = |-1 0 0||y|
|z’| | 0 0 1| | 0 0 1||z| | 0 0 1||z|
Applying an additional threefold rotation results in the identity
C32C31 = C33=E
|x’| | -1 1 0| | 0 -1 0||x| |1 0 0||x|
|y’| = | -1 0 0| | 1 -1 0||y| = |0 1 0||y|
|z’| | 0 0 1| | 0 0 1||z| |0 0 1||z|
Symbols used in the description of symmetry in the International Tables for Crystallography:
for 3-fold axis
Orthogonal to the sheet or along the Diagonals of a cube:


E.g., triphenylphosphine.
Fourfold axis

Fourfold axis (proper axis of order 4) = rotations of 360/4 = 90°
If the rotation axis is along the z-axis, the point with coordinates x,y,z has as its first symmetry-equivalent point the point with coordinates −y,x,z.
In matrix form, a 90° rotation around the z-axis can be represented by the following matrix:
|x’| |0 -1 0| |x|
|y’| = |1 0 0| |y|
|z’| |0 0 1| |z|
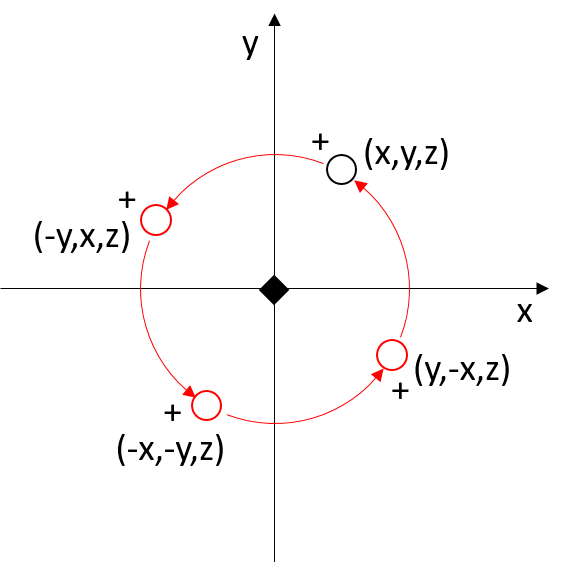
Applying the fourfold rotation twice is equivalent to a twofold rotation
C41C41 = C42 = C21
|x’| | 0 -1 0| |0 -1 0||x| |-1 0 0||x|
|y’| = |1 0 0| |1 0 0||y| = | 0 -1 0||y|
|z’| | 0 0 1| |0 0 1||z| | 0 0 1||z|
Applying the fourfold rotation operation three times generates a third symmetry-equivalent point with coordinates y,−x,z.
C41C41C41 = C43
|x’| |-1 0 0| |0 -1 0||x| | 0 1 0||x|
|y’| = |0 -1 0| |1 0 0||y| = |-1 0 0||y|
|z’| |0 0 1| |0 0 1||z| | 0 0 1||z|
Applying an additional fourfold rotation results in the identity
C41C41C41C41 = C44 = E
|x’| | 0 1 0| |0 -1 0||x| |1 0 0||x|
|y’| = |-1 0 0| |1 0 0||y| = |0 1 0||y|
|z’| |0 0 1| |0 0 1||z| |0 0 1||z|
Symbols used in the description of symmetry in the International Tables for Crystallography
for 4-fold axis
Orthogonal and Parallel to the sheet plane:

E.g. Porphyrin
Sixfold axis

Sixfold axis (proper axis of order 6) = rotations of 360/6 = 60°
If the rotation axis element is along the z-axis and a hexagonal coordinate system is used (with the angle γ between the x and y axes = 120°), the point with coordinates x,y,z has as its first symmetry-equivalent point the point with coordinates x−y,x,z.
In matrix form, a 60° rotation around the z-axis in a hexagonal system can be represented by the following matrix:
|x’| | 1 -1 0| |x|
|y’| = | 1 0 0| |y|
|z’| | 0 0 1| |z|
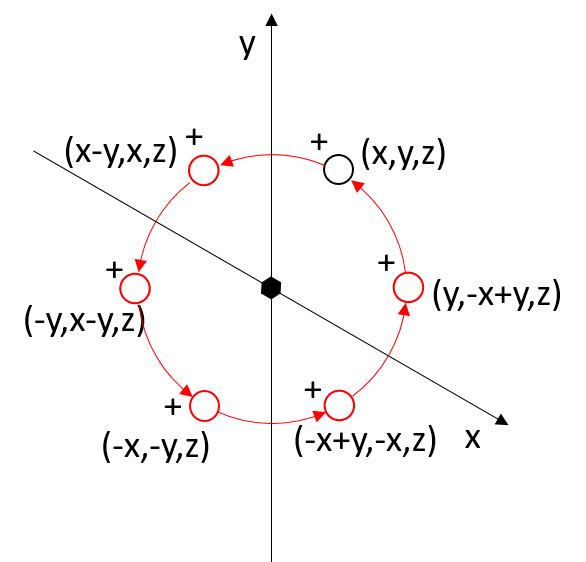
Applying the sixfold rotation twice generates a second symmetry-equivalent point with coordinates −y,x−y, z equivalent to a threefold rotation.
C61C61 = C62 = C31
|x’| | 1 -1 0| | 1 -1 0||x| | 0 -1 0||x|
|y’| = | 1 0 0| | 1 0 0||y| = | 1 -1 0||y|
|z’| | 0 0 1| | 0 0 1||z| | 0 0 1||z|
Applying an additional rotation operation of order 6 generates a third symmetry-equivalent point with coordinates −x,−y,z-x, -y, z which is equivalent to a twofold rotation.
C62C61 = C63= C21
|x’| | 0 -1 0| | 1 -1 0||x| |-1 0 0||x|
|y’| = | 1 -1 0| | 1 0 0||y| = |0 -1 0||y|
|z’| | 0 0 1| | 0 0 1||z| |0 0 1||z|
An additional rotation operation of order 6 generates a fourth symmetry-equivalent point with coordinates −x+y,−x,z-x + y, -x, z equivalent to the second threefold rotation.
C63C61 = C64= C32
|x’| |-1 0 0| | 1 -1 0||x| |-1 1 0||x|
|y’| = | 0 -1 0| | 1 0 0||y| = |-1 0 0||y|
|z’| | 0 0 1| | 0 0 1||z| | 0 0 1||z|
Applying the fifth consecutive rotation of order 6 generates a fifth symmetry-equivalent point with coordinates y,−x+y,z.
C64C61 = C65
|x’| |-1 1 0| | 1 -1 0||x| | 0 1 0||x|
|y’| = |-1 0 0| | 1 0 0||y| = |-1 1 0||y|
|z’| | 0 0 1| | 0 0 1||z| |0 0 1||z|
Applying the final rotation of order 6 brings the point back to the starting position, thus resulting in the identity.
C65C61 = C66= E
|x’| | 0 1 0| | 1 -1 0||x| |1 0 0||x|
|y’| = |-1 1 0| | 1 0 0||y| = |0 1 0||y|
|z’| | 0 0 1| | 0 0 1||z| | 0 0 1||z|
Symbols used in the description of symmetry in the International Tables for Crystallography
for 6-fold axis
Orthogonal to the sheet plane:

E.g., alpha-cyclodextrin
The 1, 2, 3, 4, and 6 axes are the only symmetry axes compatible with the crystal lattices.
Other symmetry axes incompatible with the crystal lattice
In contrast to crystals, molecules can have other rotation axes, such as the C5 axis.
Principal Axis
A molecule can have more than one symmetry axis (or crystals can have more than one direction with symmetry axes). The highest-symmetry axis (or direction) in a molecule (or crystal) is called the principal axis and it is usually aligned with the molecular z-axis (or in crystals, the c-axis in the tetragonal and hexagonal crystal families, or the b-axis in the monoclinic family). Having higher symmetry means generating more symmetry-equivalent points.
Plane of Symmetry
The symmetry element is a plane, and the symmetry operation is the reflection through the plane.
If the symmetry plane contains the a and c axes and is orthogonal to b, a point with coordinates x,y,z has its symmetry-equivalent point at x,−y,z.
In matrix form this reflection can be represented by the following matrix:
|x’| | 1 0 0| |x|
|y’| = | 0 -1 0| |y|
|z’| | 0 0 1| |z|
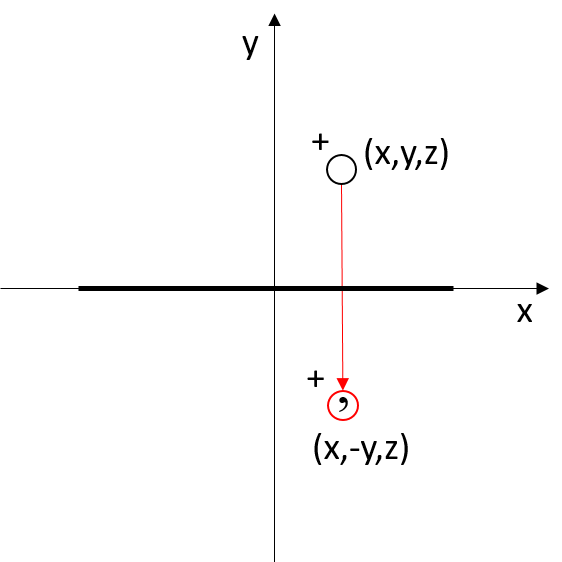
Applying the reflection operation twice results in the identity.
|x’| |1 0 0| |1 0 0||x| |1 0 0||x|
|y’| = |0 -1 0| |0 -1 0||y| = |0 1 0||y|
|z’| |0 0 1| |0 0 1||z| |0 0 1||z|
The mirror reflection symmetry operation m corresponds to the rotoinversion symmetry operation of order two 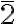 relative to an axis that intersects the plane perpendicularly at the inversion center.
relative to an axis that intersects the plane perpendicularly at the inversion center.
|x’| | -1 0 0| |-1 0 0| |x| | 1 0 0| |x|
|y’| = | 0 -1 0| | 0 -1 0| |y| = | 0 1 0| |y|
|z’| | 0 0 1| | 0 0 -1| |z| | 0 0 -1| |z|
E.g., Thionyl chloride.
Improper Rotations
Improper rotations are a combination of a rotation operation around an axis followed by either:
Reflection through a plane perpendicular to the axis (roto-reflection operation), or
Inversion through a point on the axis (roto-inversion operation).
Although these two types of improper rotations differ, they are equivalent ways of describing point symmetry.
In crystallography, the Hermann-Mauguin notation is used, which is based on roto-inversion symmetry;
The Schoenflies notation, commonly used for describing molecular point symmetry, is based on roto-reflection symmetry.
The geometric symmetry elements associated with improper rotations can be a point, an axis, or a plane, depending on the type of improper rotation.
Roto-inversion
In crystallographic symmetry, roto-inversion operations are considered. These consist of a rotation around an axis followed by an inversion through a point on the same axis.
The axis is called improper because, as we will see, the symmetry element can correspond to either a point or a geometric plane.
The cases to be considered are those compatible with the translational symmetry of the crystallographic unit cell: axes of order 1, 2, 3, 4, and 6.
Roto-inversion of Order 1
The roto-inversion of order 1 (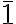 ) corresponds, as previously mentioned, to the inversion center and is associated with the inversion point symmetry element. Therefore, in this case, the direction of the axis is irrelevant.
) corresponds, as previously mentioned, to the inversion center and is associated with the inversion point symmetry element. Therefore, in this case, the direction of the axis is irrelevant.
Roto-inversion of Order 2
The roto-inversion of order 2 (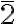 , denoted as m) corresponds, as previously mentioned, to reflection through a plane perpendicular to the improper axis. It is therefore associated with the mirror plane symmetry element (m). The roto-inversion axis is thus orthogonal to the symmetry plane. This symmetry element relates the two enantiomorphous halves of space separated by the plane.
, denoted as m) corresponds, as previously mentioned, to reflection through a plane perpendicular to the improper axis. It is therefore associated with the mirror plane symmetry element (m). The roto-inversion axis is thus orthogonal to the symmetry plane. This symmetry element relates the two enantiomorphous halves of space separated by the plane.
Important Note:
The mirror plane symmetry element (m) is not equivalent to the simultaneous presence of a 2-fold rotation axis (2) and an inversion center 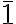 .
.
This combination of symmetry operations is denoted as 2/m and corresponds to the simultaneous presence of a 2-fold axis and a perpendicular mirror plane (m) intersecting at the inversion center 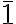 .
.
These symmetry operations relate four equivalent points, which are paired according to their symmetry relation by a 2-fold rotation axis (2), an inversion center (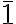 ), and a mirror plane (m).
), and a mirror plane (m).
E.g., (δ,λ)-trans-[Co(en)₂Cl₂]⁺ (point symmetry 2/m or C₂h)
The symbol used in the International Tables of Crystallography for the 2/m symmetry is a combination of the twofold axis and the inversion center symbols.
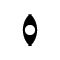
Roto-inversion of Order 3
The roto-inversion of order 3 ( 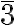 ) is equivalent to the combination of a 3-fold rotation and an inversion center
) is equivalent to the combination of a 3-fold rotation and an inversion center 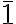 present on the axis. Therefore, it is equivalent to the simultaneous presence of a 3-fold axis and an inversion center
present on the axis. Therefore, it is equivalent to the simultaneous presence of a 3-fold axis and an inversion center 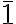 . This symmetry element relates 6 equivalent points in space (two enantiomorphic triplets).
. This symmetry element relates 6 equivalent points in space (two enantiomorphic triplets).
In Hermann-Mauguin notation (also called International Notation, as it is adopted by the International Tables for Crystallography), if two or more axes share the same direction, only the axis with the higher symmetry is indicated.
If the roto-inversion axis is aligned along the z-axis and a hexagonal coordinate system is used (with an angle γ between the x and y axes of 120°), a point with coordinates x,y,z has its first symmetry-equivalent point at y,−x+y,−z, which is indirect congruent to the original point due to the inversion operation.
In matrix terms:
|x’| |0 -1 0| |-1 0 0||x| | 0 1 0||x|
|y’| = |1 -1 0| | 0 -1 0||y| = |-1 1 0||y|
|z’| |0 0 1| | 0 0 -1||z| | 0 0 -1||z|
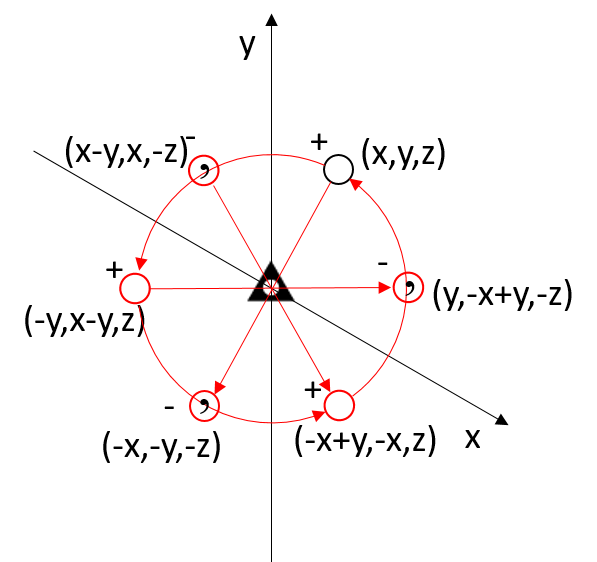
Applying the roto-inversion operation twice generates a second symmetry-equivalent point with coordinates −x+y,−x,z, which is equivalent to the second ternary rotation since the double inversion is equivalent to the identity.
|x’| | 0 1 0| | 0 1 0||x| |-1 1 0||x|
|y’| = |-1 1 0| |-1 1 0||y| = |-1 0 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| | 0 0 1||z|
An additional roto-inversion operation generates a third symmetry-equivalent point with coordinates −x,−y,−z, equivalent to an inversion operation through the center.
|x’| |-1 1 0| | 0 1 0||x| |-1 0 0||x|
|y’| = |-1 0 0| |-1 1 0||y| = |0 -1 0||y|
|z’| | 0 0 1| | 0 0 -1||z| |0 0 -1||z|
An additional roto-inversion operation generates a fourth symmetry-equivalent point with coordinates −y,x−y,z, equivalent to the first ternary rotation.
|x’| |-1 0 0| | 0 1 0||x| |0 -1 0||x|
|y’| = | 0 -1 0| |-1 1 0||y| = |1 -1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| | 0 0 1||z|
The fifth consecutive roto-reflection generates a fifth symmetry-equivalent point with coordinates x−y,x,−z.
|x’| | 0 -1 0| | 0 1 0||x| |1 -1 0||x|
|y’| = | 1 -1 0| |-1 1 0||y| = |1 0 0||y|
|z’| | 0 0 1| | 0 0 -1||z| |0 0 -1||z|
The final roto-inversion returns the point to the initial one, thus resulting in the identity.
|x’| | 1 -1 0| | 0 1 0||x| |1 0 0||x|
|y’| = | 1 0 0| |-1 1 0||y| = |0 1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| |0 0 1||z|
The symbol used in the description of symmetry in the International Tables of Crystallography
with the 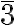 axis orthogonal to the sheet:
axis orthogonal to the sheet:

E.g., [Co(hexacyclen)]³⁺ (point symmetry 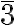 o S6)
o S6)
Roto-inversion of Order 4
The roto-inversion of order 4 ( 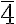 ), unlike the previous case, is not equivalent to the product of a 4-fold rotation and an inversion center
), unlike the previous case, is not equivalent to the product of a 4-fold rotation and an inversion center 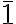 . This symmetry element relates 4 equivalent points in space. The improper roto-inversion axis
. This symmetry element relates 4 equivalent points in space. The improper roto-inversion axis 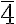 also coincides with a proper 2-fold axis, which is not indicated (see above).
also coincides with a proper 2-fold axis, which is not indicated (see above).
If the rotation axis is along the z-axis, a point with coordinates x,y,z has its first symmetry-equivalent point at y,−x,−z, which is indirectly congruent.
In matrix:
|x’| |0 -1 0| |-1 0 0||x| | 0 1 0||x|
|y’| = |1 0 0| | 0 -1 0||y| = |-1 0 0||y|
|z’| |0 0 1| | 0 0 -1||z| | 0 0 -1||z|
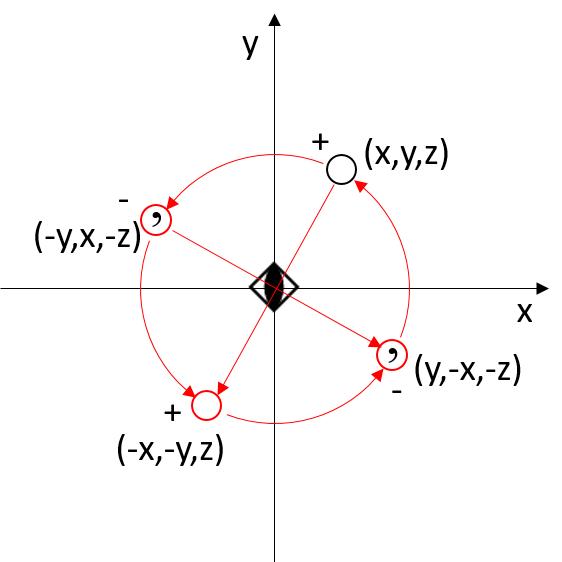
The application of the quaternary roto-inversion operation twice is equivalent to a twofold rotation.
|x’| | 0 1 0| | 0 1 0||x| |-1 0 0||x|
|y’| = |-1 0 0| |-1 0 0||y| = | 0 -1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| | 0 0 1||z|
The application of the quaternary roto-inversion operation three times generates a third symmetry-equivalent point with coordinates −y,x,−z
|x’| |-1 0 0| | 0 1 0||x| | 0 -1 0||x|
|y’| = |0 -1 0| |-1 0 0||y| = | 1 0 0||y|
|z’| |0 0 1| | 0 0 -1||z| | 0 0 -1||z|
The application of an additional roto-inversion operation results in the identity.
|x’| | 0 1 0| |0 -1 0||x| |1 0 0||x|
|y’| = |-1 0 0| |1 0 0||y| = |0 1 0||y|
|z’| |0 0 1| |0 0 1||z| |0 0 1||z|
Symbols used in the description of this symmetry in the International Tables of Crystallography
Orthogonal to the sheet and along a diagonal.

E.g., Bis(2,5-dithiahexane) copper(I) complex (point symmetry 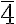 o S4)
o S4)
Roto-inversion of Order 6
The roto-inversion of order 6 ( 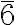 ) is equivalent to the product of a 3-fold rotation and a reflection plane (m) orthogonal to the axis. Thus, it corresponds to the simultaneous presence of a proper 3-fold axis and an m reflection plane orthogonal to the axis (3/m). This combination of symmetry elements relates 6 equivalent points in space. In the International notation, it is indicated as
) is equivalent to the product of a 3-fold rotation and a reflection plane (m) orthogonal to the axis. Thus, it corresponds to the simultaneous presence of a proper 3-fold axis and an m reflection plane orthogonal to the axis (3/m). This combination of symmetry elements relates 6 equivalent points in space. In the International notation, it is indicated as 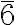 and not 3/m (see above).
and not 3/m (see above).
If the roto-inversion axis is along the z-axis and a hexagonal coordinate system is used (with the angle γ\gammaγ between the x and y axes equal to 120°), a point with coordinates x,y,z has its first symmetry-equivalent point at −x+y,−x,−z, which is indirectly congruent to the original point due to the inversion operation.
In matrix:
|x’| |1 -1 0| |-1 0 0||x| |-1 1 0||x|
|y’| = |1 0 0| | 0 -1 0||y| = |-1 0 0||y|
|z’| |0 0 1| | 0 0 -1||z| |0 0 -1||z|
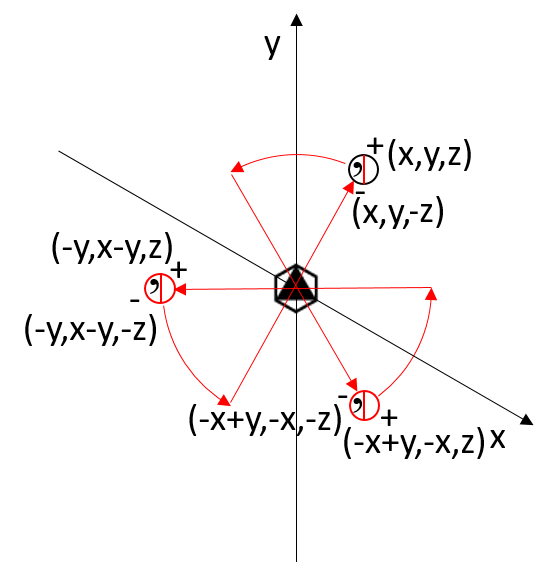
The application of the roto-inversion operation twice generates a second symmetry-equivalent point with coordinates −y,x−y,z which is equivalent to the first 3-fold rotation, since a double inversion is equivalent to the identity.
|x’| |-1 1 0| |-1 1 0||x| |0 -1 0||x|
|y’| = |-1 0 0| |-1 0 0||y| = |1 -1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| |0 0 1||z|
An additional roto-inversion operation generates a third symmetry-equivalent point with coordinates x,y,−z, which corresponds to a reflection operation through a plane perpendicular to the improper axis.
 2
2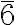 1 =
1 = 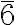 3=
3= 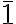 161
161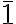 161
161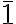 161=
161= 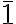 163=
163= 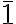 121 =
121 = 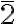 1 = m1
1 = m1
|x’| | 0 -1 0| |-1 1 0||x| |1 0 0||x|
|y’| = | 1 -1 0| |-1 0 0||y| = |0 1 0||y|
|z’| | 0 0 1| | 0 0 -1||z| |0 0 -1||z|
An additional roto-inversion operation generates a fourth symmetry-equivalent point with coordinates −x+y,−x,z, equivalent to the second threefold rotation.
|x’| |1 0 0| |-1 1 0||x| |-1 1 0||x|
|y’| = |0 1 0| |-1 0 0||y| = |-1 0 0||y|
|z’| |0 0 -1| | 0 0 -1||z| | 0 0 1||z|
The fifth consecutive roto-reflection generates a fifth symmetry-equivalent point with coordinates −y,x−y,−z.
|x’| |-1 1 0| |-1 1 0||x| |0 -1 0||x|
|y’| = |-1 0 0| |-1 0 0||y| = |1 -1 0||y|
|z’| | 0 0 1| | 0 0 -1||z| |0 0 -1||z|
The final roto-inversion brings the point back to the starting position, thus resulting in the identity.
|x’| | 0 -1 0| |-1 1 0||x| |1 0 0||x|
|y’| = | 1 -1 0| |-1 0 0||y| = |0 1 0||y|
|z’| | 0 0 -1| | 0 0 -1||z| |0 0 1||z|
The symbol in the International Tables for Crystallography
Orthogonal to the plane.

E.g.,Triethylborane (point symmetry 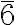 o C3h)
o C3h)
Roto-reflections
In Schoenflies notation, which is more commonly used to describe molecular symmetry, improper axes are represented by roto-reflections.
Improper roto-reflection axes of order n, which correspond to a rotation of 360°/n around the axis followed by a reflection through a perpendicular plane, are denoted as Sₙ (from the German Spiegel, meaning mirror).
The improper roto-reflection axis of order 1, S₁, coincides with the symmetry plane σ (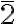 = m).
= m).
The improper roto-reflection axis of order 2, S₂, coincides with the inversion center i (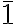 ).
).
The improper roto-reflection axis of order 3, S₃, is equivalent to the roto-inversion axis 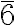 .
.
The improper roto-reflection axis of order 4, S₄, is equivalent to the roto-inversion axis 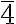 .
.
The improper roto-reflection axis of order 6, S₆, is equivalent to the roto-inversion axis 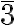 .
.
Notably:
the two types of improper axes of order 4 coincide: S₄ = 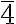 .
.
Both roto-inversion and roto-reflection axes relate indirectly congruent objects (enantiomorphs).
Chiral (asymmetric or dissymmetric) molecules do not possess improper axes.


