Point Symmetry Groups for Molecules and Crystals
Notation of point symmetry elements
Symmetry Elements Schoenflies (molecules) Hermann–Mauguin (crystallography)
Proper Axis of Order n Cn n
Improper Axis of Order n Sn retroreflection 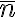 rotoinversion
rotoinversion
Special Improper Axis S1 = σ S2 = i 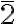 = m
= m
Correspondence between improper axes S1(σ)=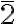 (m); S2(i)=
(m); S2(i)=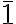 ; S3=
; S3=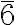 ; S4=
; S4=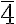 ; S6=
; S6=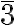
Given a symmetry operation associated with a proper or improper axis, Xm, the inverse symmetry operation, which brings the object back to its original state, always exists:
In matrix terms, this corresponds to the inverse matrix of the symmetry operation Xm.
The application of a symmetry operation followed by its inverse operation returns the system to its initial state, resulting in the identity:
XmX-m= X0 = 1 (E)
In mathematics, a group is an algebraic structure consisting of a set of elements equipped with an internal binary operation (which combines two elements of the group to produce another element of the group, such as multiplication * or addition +) that satisfies the following axioms:
1) Existence of a neutral element (identity):
There exists a neutral element E (or unit 1) such that for every element X in the group, applying the binary operation with E produces X itself:
E∗X=X
2) Existence of an inverse element:
For every element X in the group, there exists an inverse element X-1 such that applying the binary operation between an element and its inverse results in the neutral element:
X*X-1=E
3) Associativity:
The binary operation is associative, meaning that for all elements A, B, C in the group, the grouping of operations does not affect the result:
(A*B)*C=A*(B*C)=A*B*C
4) Closure:
For all elements in the group, the result of applying the internal binary operation to any two elements remains within the group.
The set of symmetry operations Xn associated with individual symmetry elements X, including the identity X0, forms a group.
Additionally, combining two or more symmetry elements can generate a group of associated symmetry operations.
In the case of point symmetry operations, the corresponding groups are called Point Symmetry Groups or Point Groups.
The number of point groups is infinite, as there are infinitely many symmetry axes, both proper and improper (where the order n of the axis is any integer number).
However, considering only the point symmetry compatible with crystal lattices (proper and improper axes of orders 1, 2, 3, 4, and 6), we obtain 32 distinct crystallographic point groups, corresponding to the 32 Crystal Classes listed by Hessel in 1830.
Each point group has a descriptive symbol that represents the presence of a specific combination of symmetry elements whose operations belong to the group.
Schoenflies Notation
The initial uppercase letter refers to the point group's principal axis of symmetry (the highest symmetry).
- C (Cyclic): A single proper axis.
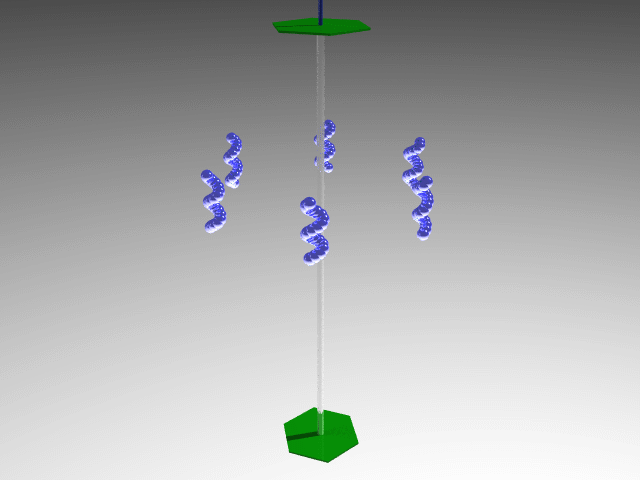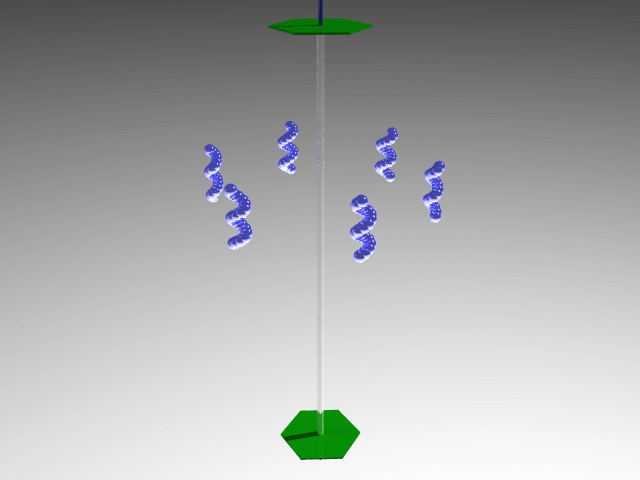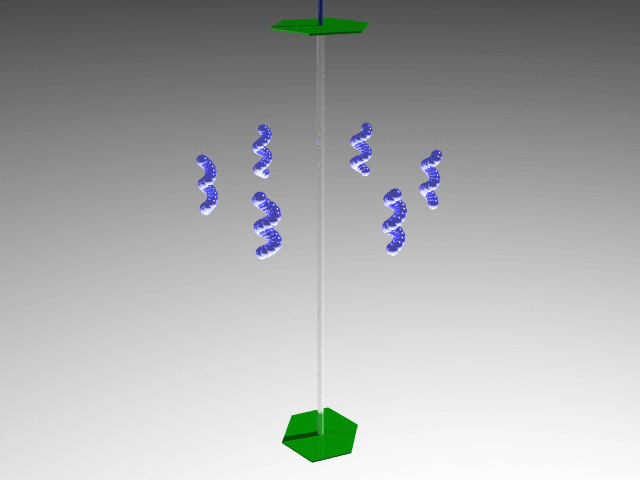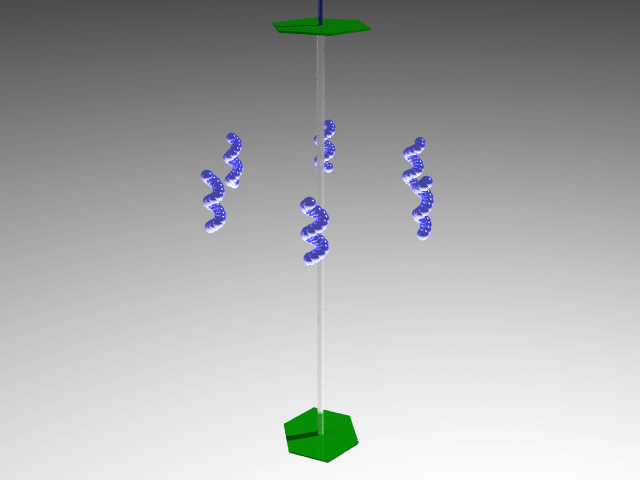
E.g., C6 point group
S (Spiegel = mirror in German): A single improper axis.

E.g., S4 point group
D (Dihedral = solid with two faces): n twofold axes orthogonal to the principal axis of n order, in addition to possible symmetry planes.
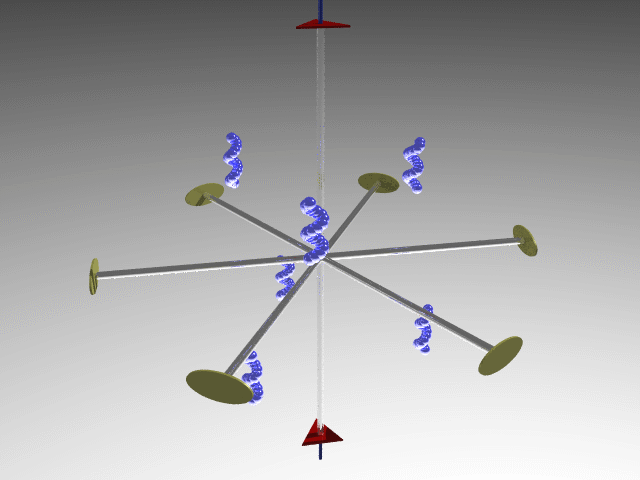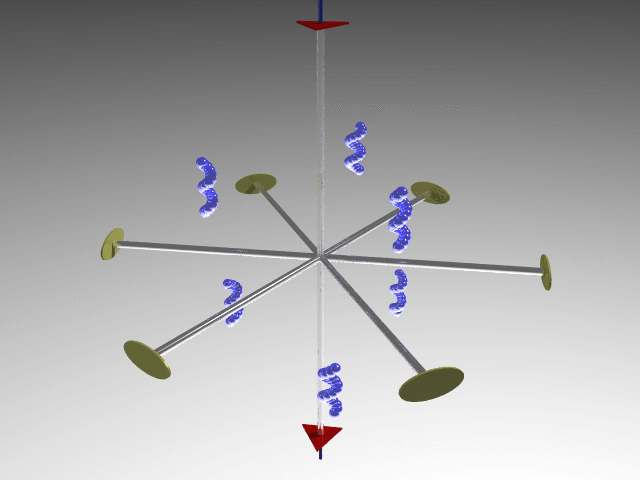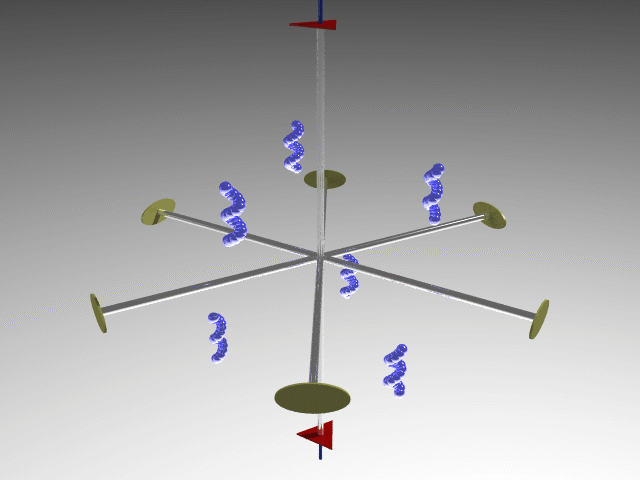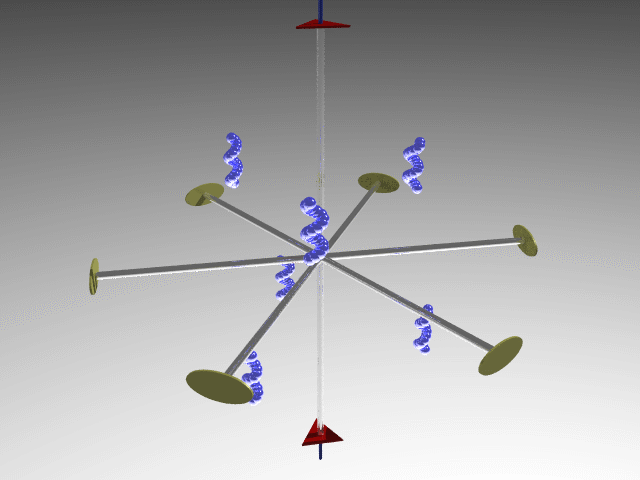
E.g., D3 point group
T (Tetrahedral = Platonic solid with four faces): Four axes of order 3 and possible further twofold axes and/or symmetry planes.
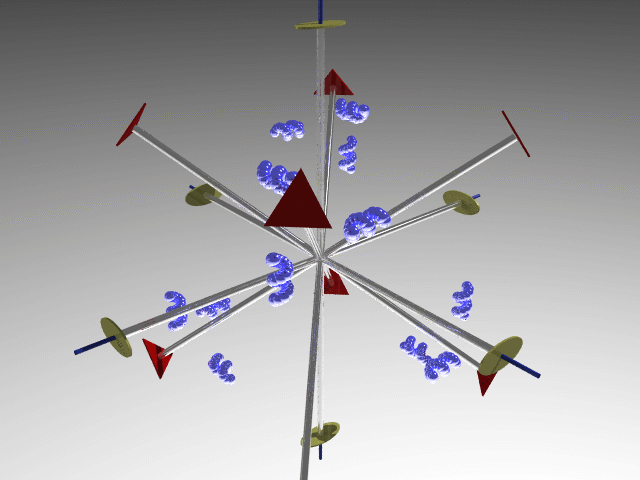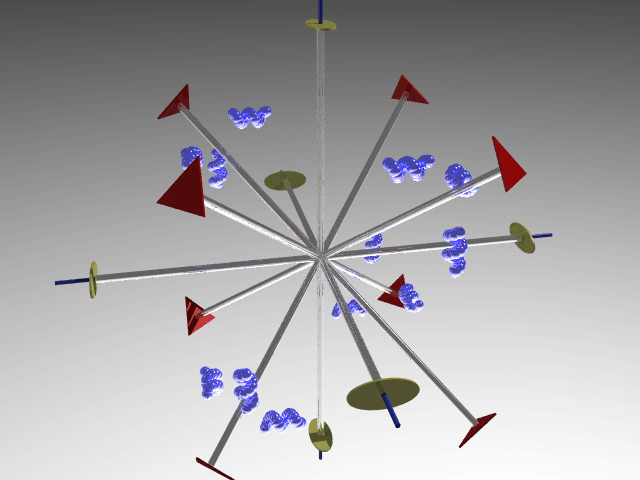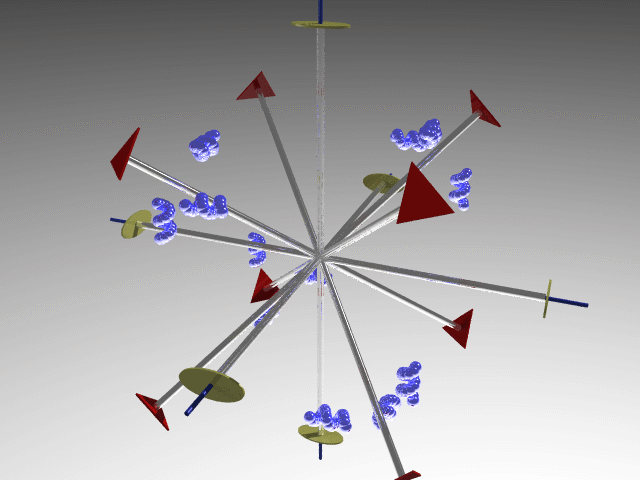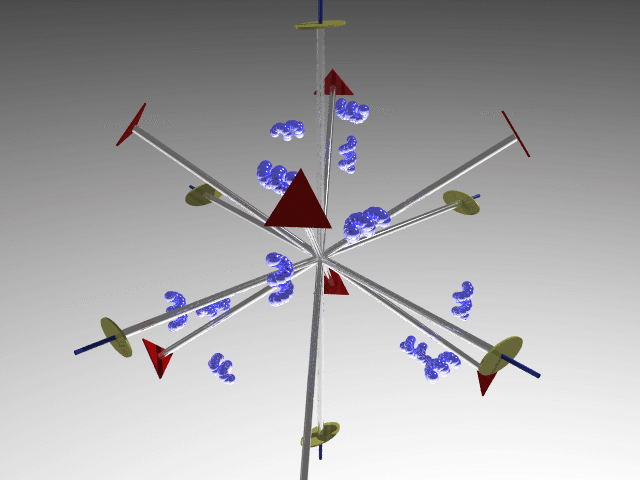
E.g., T point group
O (Octahedral = Platonic solid with eight faces): Three fourfold axes and possible other lower-order axes and/or symmetry planes.
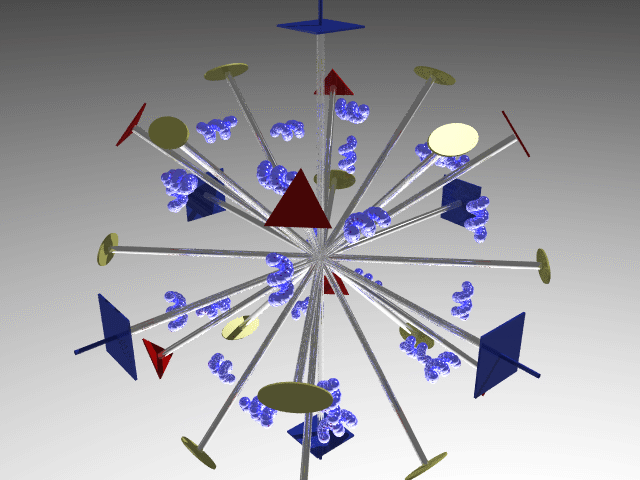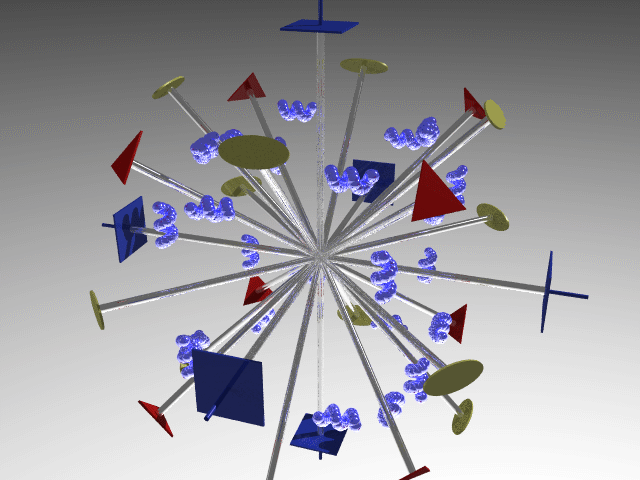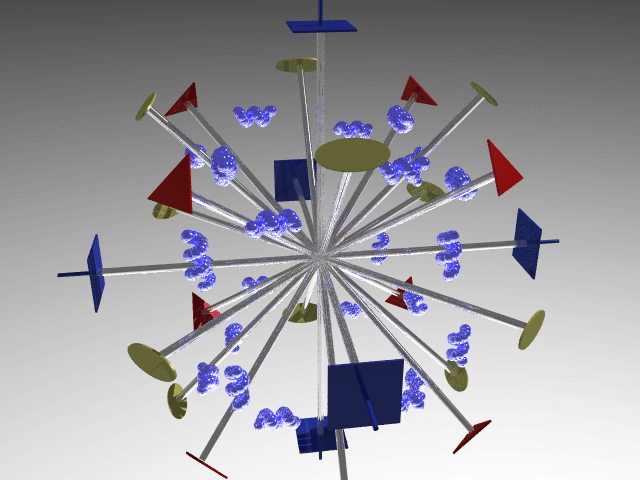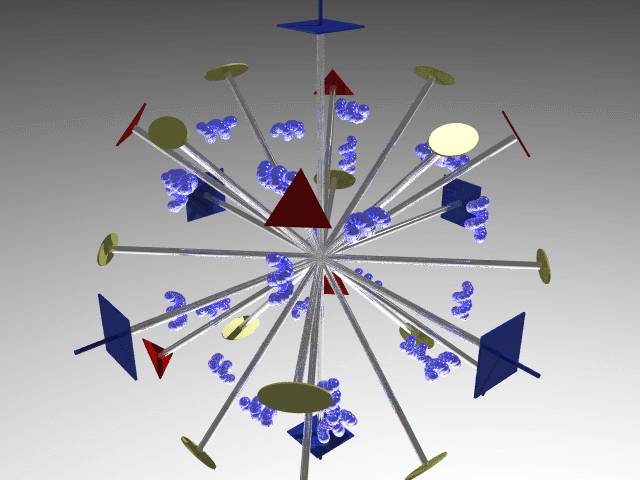
E.g., O point group
I (Icosahedral = Platonic solid with twenty faces): Generated by six axes of order 5 and other lower-order axes and/or symmetry planes. Icosahedral point groups are not compatible with crystallographic symmetry due to the presence of axes of order 5.
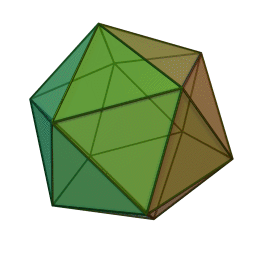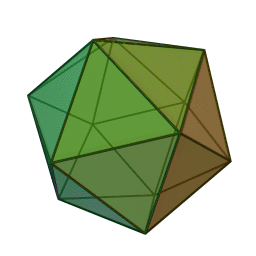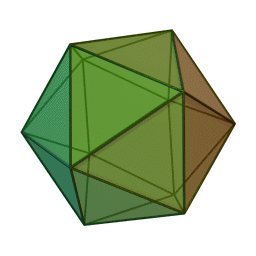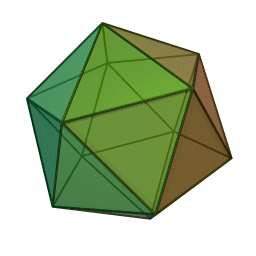
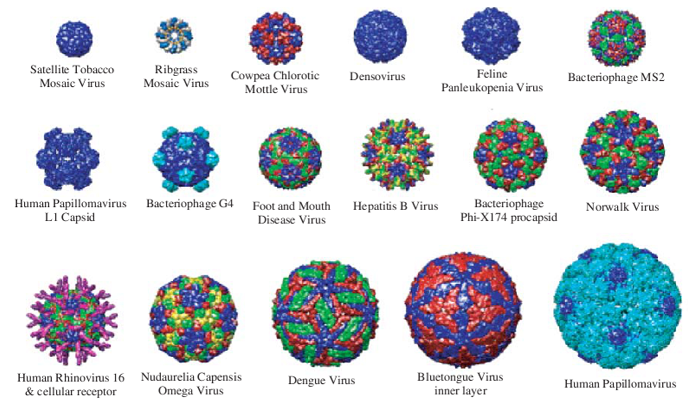
This type of symmetry is quite common in viruses.
In Schoenflies notation for point groups, the numerical subscript attached to the initial uppercase letter (C, S, D, etc.) represents the order of the principal rotation axis
For example:
- C₄: A point group with a fourfold rotation axis.
- D₃: A point group with a threefold principal rotation axis and dihedral symmetry (three orthogonal twofold axes).
- S₆: A point group with a sixfold improper rotation axis (rotoreflection).
An additional subscript indicates the presence of certain types of symmetry planes:
v = vertical mirror planes containing the principal axis σv
h = horizontal mirror plane perpendicular to the principal axis σh
d = diagonal mirror plane that contains the principal axis and bisects the orthogonal twofold axes σd
For example:
- C2v: A point group with one twofold rotation axis (C₂) and two vertical mirror planes (σv) that contain the principal axis.
- C₃h: A point group with one threefold rotation axis (C₃) and one horizontal mirror plane (σh) perpendicular to the principal axis.
- D2d: A point group with one principal twofold axis (C₂), two perpendicular C₂ axes, two diagonal mirror planes (σd) that contain the principal axis and bisect the two perpendicular axes, and one improper fourfold axis (S₄) along the principal axis. The S₄ rotoreflection symmetry arises naturally from the combination of other symmetry elements and, therefore, it is not explicitly indicated in the symbol of the point group because it is considered a derived symmetry rather than a primary one.
The subscript i is used when only the inversion element, i, is present along with the identity (Ci).
The subscript s is used when it is present only the mirror plane element, σ, along with the identity (Cs).
The subscript ∞ is used for linear molecules with an infinite order axis (C∞).
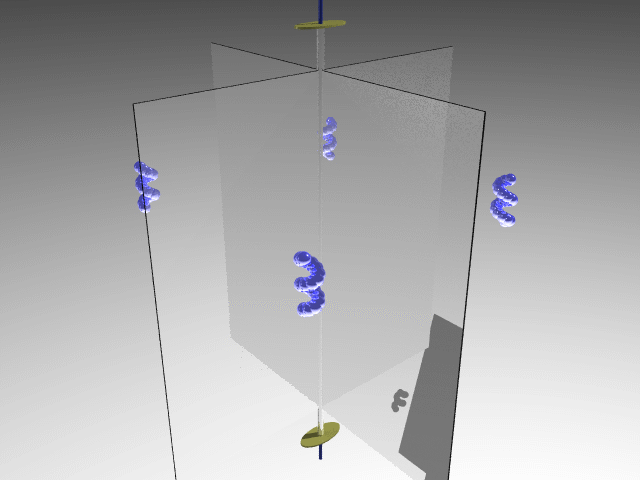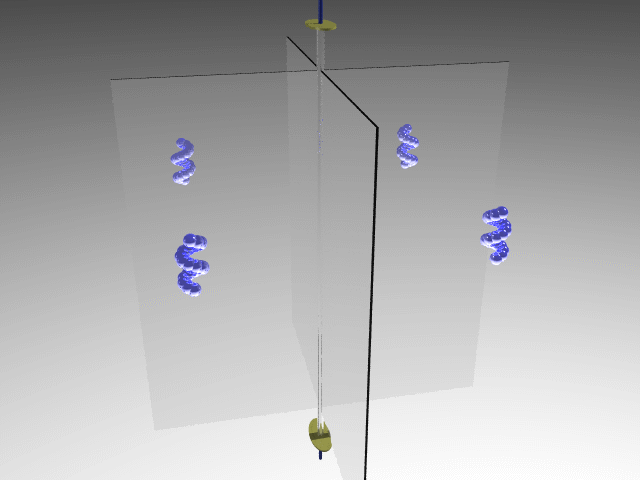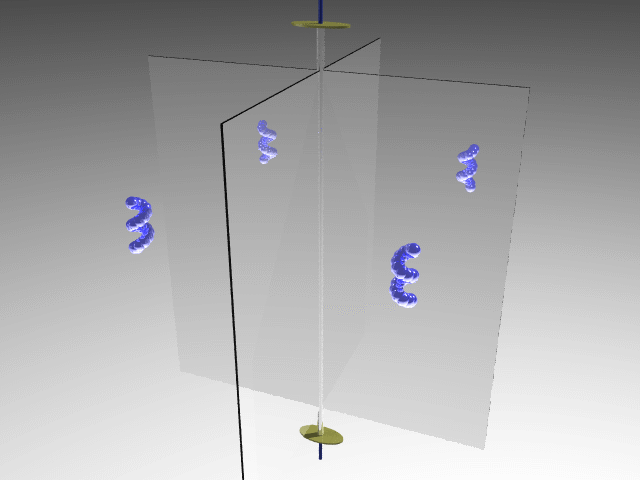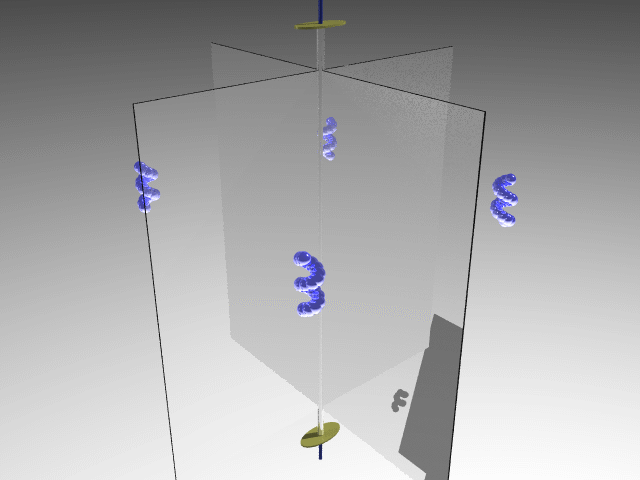
E.g., Dichloromethane

E.g., trans-dichloroethylene
For Groups with a Single Principal Axis of Order Higher than 2
The symbols of the symmetry elements are arranged sequentially according to a set of three components, which indicate:
The first position: indicates the symmetry of the principal axis.
The second position: indicates the symmetry along the orthogonal (secondary) direction.
The third position: indicates the symmetry along the diagonal between the secondary directions.
Example:
- 4 2 2 represents a point group with:
- A principal axis of order 4.
- A twofold axis in the orthogonal direction (which is doubled due to the fourfold symmetry).
- A twofold axis along the diagonal between the two secondary axes (which also doubles due to the fourfold symmetry).
- In total, this results in one fourfold axis and four orthogonal twofold axes, corresponding to D₄ in Schoenflies notation.
E.g., tetrathiocyclododecane
For High-Symmetry Groups (more axes of order higher than 2)
For example, cubic symmetry groups have 4 axes of order 3 along the diagonals of the cube:
The first position: indicates the symmetry along the x direction (which is also equivalent, by symmetry, to the y and z directions).
The second position: indicates the symmetry along the diagonal directions.
The third position: indicates the symmetry along the midpoint of the x, y directions (which is also equivalent, by symmetry, to the diagonals x, z, and y, z).
Example:
- 4 3 2 represents a point group with:
- fourfold axes along the three equivalent x, y, and z directions,
- threefold axes along the 4 diagonals of the cube,
- twofold axes along the 6 face diagonals of the cube.
- This corresponds to the O (octahedral) point group in Schoenflies notation
E.g., dodeca(ethylene)octamine
In the international notation of the point group, only the symmetry elements that characterize the group are generally explicitly indicated. The additional symmetry elements that are implicitly generated from the symmetry elements characterizing the group are not indicated in the symbol.
