Crystallographic Point Symmetry Groups (Crystal Classes)
The 32 crystallographic point symmetry groups
By considering only the point symmetry of proper and improper axes of order 1, 2, 3, 4, and 6 compatible with crystal lattices, the 32 Crystal Classes are obtained.
Two symmetry classes are obtained with only the identity operation 1 or the identity plus the inversion operation 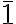 .
.
These two classes, one non-centrosymmetric and one centrosymmetric, belong to the
Triclinic system:


Three symmetry classes are obtained from the presence of a twofold rotation axis, which can be either a proper axis (2), an improper axis ((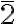 ), i.e. mirror plane m), or both (2/m). In the latter case, an inversion center is also generated. These three classes, two non-centrosymmetric and one centrosymmetric, belong to the
), i.e. mirror plane m), or both (2/m). In the latter case, an inversion center is also generated. These three classes, two non-centrosymmetric and one centrosymmetric, belong to the
Monoclinic system:
2 (C2); m (Cs); 2/m (C2h)



Three symmetry classes are obtained by orthogonally combining multiple twofold axes.
Orthogonally combining two proper symmetry axes of order 2 generates a third 2-fold axis, orthogonal to the others. The symmetry operations related to these three orthogonal twofold axes define the 222 point group.
Orthogonally combining a proper symmetry axis of order 2 with an improper rotation axis 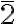 (mirror plane m) generates a second improper rotation axis
(mirror plane m) generates a second improper rotation axis 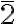 (mirror plane m) orthogonally. The symmetry operations related to these two orthogonal mirror planes containing the twofold axis define the mm2 point group.
(mirror plane m) orthogonally. The symmetry operations related to these two orthogonal mirror planes containing the twofold axis define the mm2 point group.
Orthogonally intersecting three improper symmetry axes 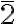 (mirror planes m) generates an inversion center
(mirror planes m) generates an inversion center 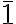 , which consequently also leads to three orthogonal twofold axes. The symmetry operations related to these three orthogonal mirror planes and three twofold axes intersecting at an inversion center define the mmm point group.
, which consequently also leads to three orthogonal twofold axes. The symmetry operations related to these three orthogonal mirror planes and three twofold axes intersecting at an inversion center define the mmm point group.
These three classes, two non-centrosymmetric and one centrosymmetric, belong to the Orthorhombic system:
222 (D2); mm2 (C2v); mmm (D2h)



Two symmetry classes are obtained from a single threefold rotation axis, which can be either a proper axis, 3, or an improper axis, 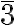 , the latter corresponding to a threefold axis combined with an inversion center.
, the latter corresponding to a threefold axis combined with an inversion center.
Three additional symmetry classes are obtained by orthogonally combining the threefold axes with either proper or improper twofold symmetry axes:
Combining a 3-fold axis with a 2-fold axis orthogonally results in two additional 2-fold axes orthogonal to the 3-fold axis. The symmetry operations related to the 3-fold axis and the three orthogonal 2-fold axes define the 32 point group.
Combining a 3-fold axis with an improper twofold axis (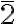 mirror plane m) orthogonally generates two additional improper twofold axes (mirror planes) orthogonal to the 3-fold axis. The symmetry operations related to the 3-fold axis and the three vertical mirror planes define the 3m point group.
mirror plane m) orthogonally generates two additional improper twofold axes (mirror planes) orthogonal to the 3-fold axis. The symmetry operations related to the 3-fold axis and the three vertical mirror planes define the 3m point group.
Combining the improper symmetry axis 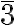 , which corresponds to a 3-fold axis plus an inversion center, with an orthogonal twofold axis, generates two additional orthogonal twofold axes at 120° each other. Due to the presence of the inversion center, three mirror planes orthogonal to these axes and containing the 3-fold axis are also generated. The symmetry operations related to these elements define the
, which corresponds to a 3-fold axis plus an inversion center, with an orthogonal twofold axis, generates two additional orthogonal twofold axes at 120° each other. Due to the presence of the inversion center, three mirror planes orthogonal to these axes and containing the 3-fold axis are also generated. The symmetry operations related to these elements define the 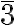 m point group.
m point group.
These five classes, three non-centrosymmetric and two centrosymmetric, belong to the
Trigonal system:




Three symmetry classes arise from a single fourfold rotation axis, which can be either a proper 4 or an improper 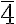 axis, and from a fourfold axis with an orthogonal symmetry plane that generates an inversion center, 4/m.
axis, and from a fourfold axis with an orthogonal symmetry plane that generates an inversion center, 4/m.
Additional symmetry classes are obtained by orthogonally combining the fourfold axes with proper or improper twofold axes. By orthogonally combining the 4-fold axis with a 2-fold axis, three additional 2-fold axes orthogonal to the 4-fold axis are obtained. The symmetry operations related to the 4-fold axis and the four orthogonal 2-fold axes define the 422 point group.
By orthogonally combining the 4-fold axis with an improper 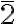 axis, three additional
axis, three additional 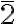 axes orthogonal to the 4-fold axis are obtained. The symmetry operations related to the 4-fold axis and the four vertical planes define the 4mm point group.
axes orthogonal to the 4-fold axis are obtained. The symmetry operations related to the 4-fold axis and the four vertical planes define the 4mm point group.
By orthogonally combining the improper 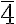 symmetry axis with a twofold axis, another twofold axis is generated orthogonally, along with two vertical planes that bisect the 2-fold axes. The symmetry operations related to these operators define the
symmetry axis with a twofold axis, another twofold axis is generated orthogonally, along with two vertical planes that bisect the 2-fold axes. The symmetry operations related to these operators define the 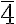 2m point group.
2m point group.
By combining the 4-fold symmetry axis with an orthogonal symmetry plane, which also generates an inversion center, with a vertical plane, three additional vertical planes are generated. The four vertical planes containing an inversion center include four twofold axes orthogonal to the 4-fold axis. The symmetry operations related to these operators define the 4/mmm point group.
These 7 classes, five non-centrosymmetric and two centrosymmetric, belong to the
Tetragonal system:


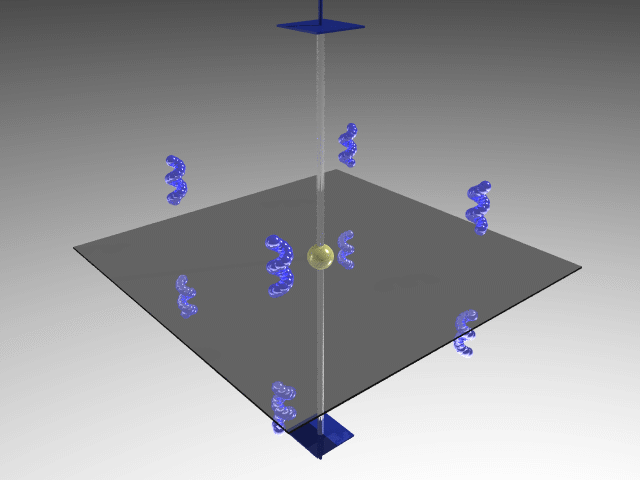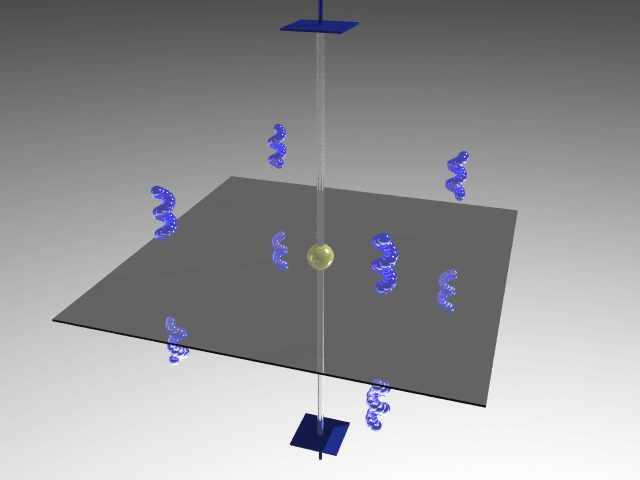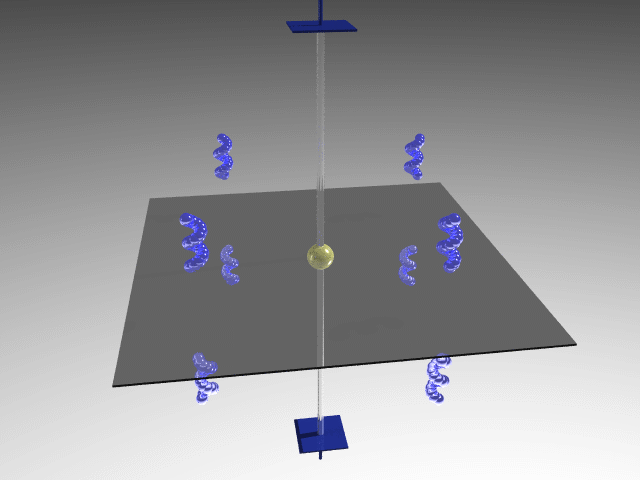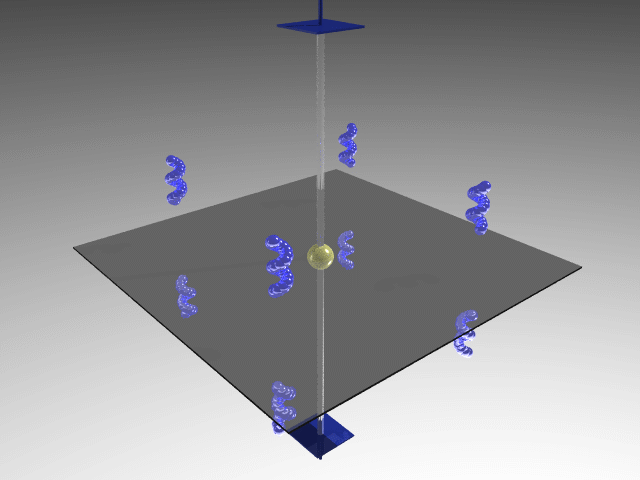
422 (D4); 4mm (C4v); 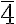 2m (D2d); 4/mmm (D4h)
2m (D2d); 4/mmm (D4h)



Three symmetry classes arise from the presence of a single hexagonal rotation axis, which can be either a proper 6 or an improper 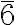 (which also corresponds to a 3-axis with an orthogonal plane, 3/m), and from a sixfold axis with an orthogonal symmetry plane that also generates an inversion center, 6/m.
(which also corresponds to a 3-axis with an orthogonal plane, 3/m), and from a sixfold axis with an orthogonal symmetry plane that also generates an inversion center, 6/m.
Four additional symmetry classes result from the orthogonal combination of order-6 axes with either proper or improper twofold symmetry axes.
By orthogonally combining the 6-axis with a 2-axis, five additional 2-axes perpendicular to the 6-axis are obtained. The symmetry operations related to the 6-axis and the six orthogonal twofold axes define the 622 point group.
By orthogonally combining the 6-axis with an improper 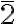 axis, five additional
axis, five additional 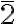 axes perpendicular to the 6-axis are obtained. The symmetry operations related to the 6-axis and the six vertical planes define the 6mm point group.
axes perpendicular to the 6-axis are obtained. The symmetry operations related to the 6-axis and the six vertical planes define the 6mm point group.
By orthogonally combining an improper symmetry axis 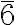 with a vertical plane, the presence of the 3-axis generates two additional vertical planes at 120°, which, when intersecting the horizontal plane, generate three additional twofold axes perpendicular to the 3-axis and contained within the three vertical planes. The symmetry operations related to these elements define the
with a vertical plane, the presence of the 3-axis generates two additional vertical planes at 120°, which, when intersecting the horizontal plane, generate three additional twofold axes perpendicular to the 3-axis and contained within the three vertical planes. The symmetry operations related to these elements define the 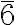 m2 point group
m2 point group
By combining the symmetry axis 6 with an orthogonal symmetry plane, which also generates an inversion center, with a vertical plane, five additional vertical planes are generated. These six vertical planes containing an inversion center include six twofold axes orthogonal to the 6-axis. The symmetry operations related to these elements define the 6/mmm point group.
These 7 classes, five non-centrosymmetric and two centrosymmetric, belong to the
Hexagonal system:


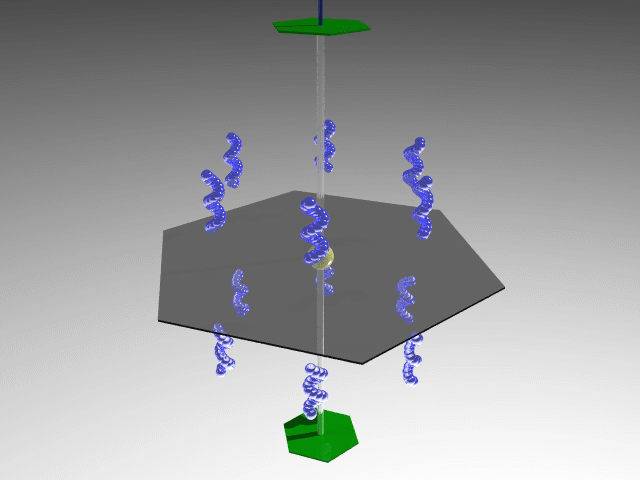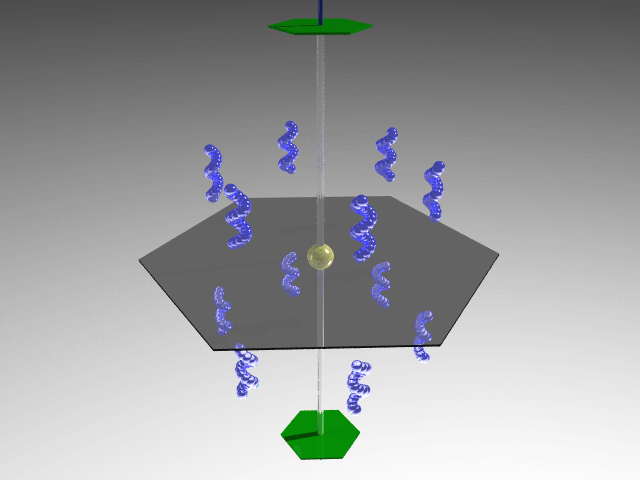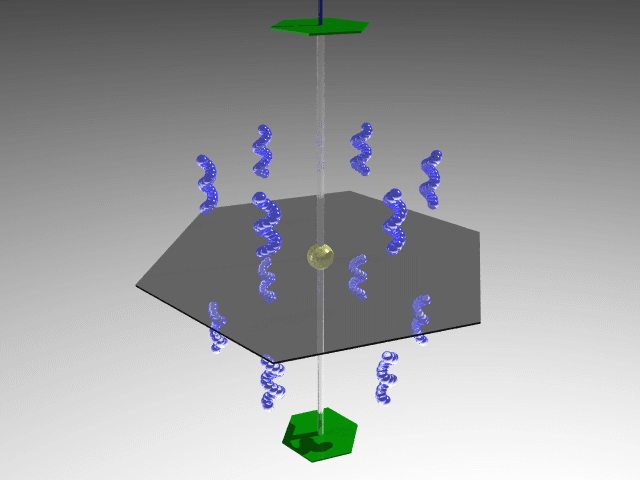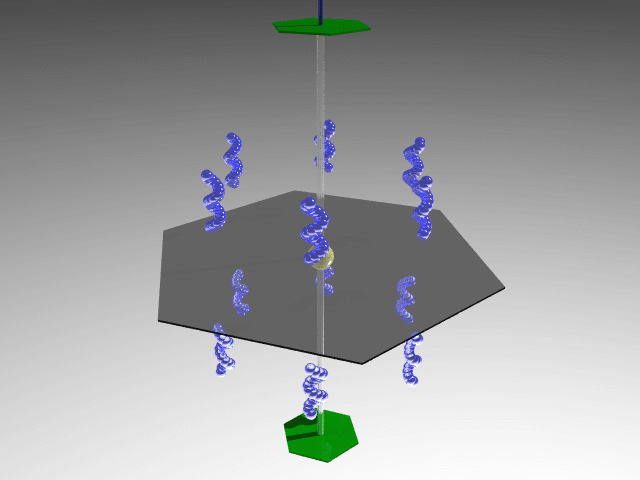
622 (D6); 6mm (C6v);  m2 (D3h); 6/mmm (D6h)
m2 (D3h); 6/mmm (D6h)
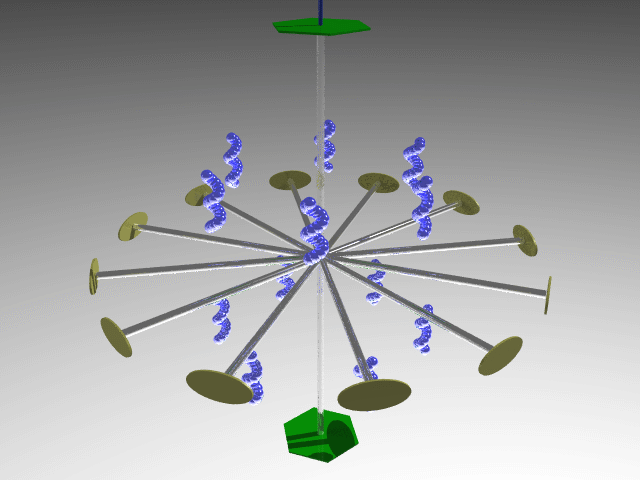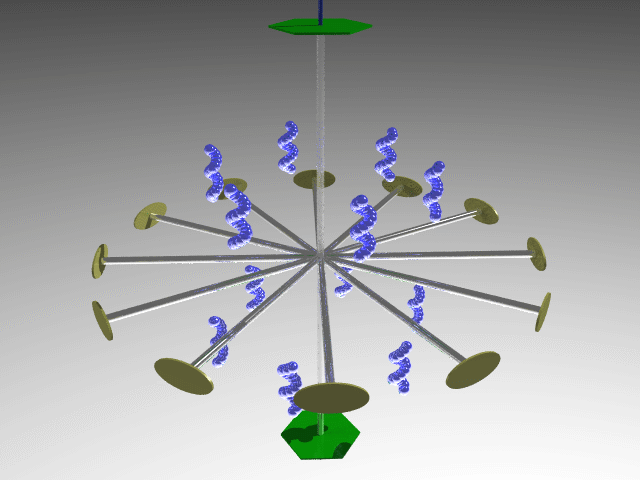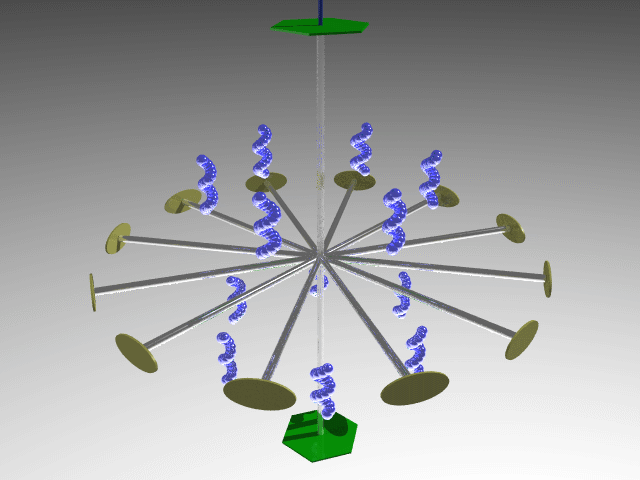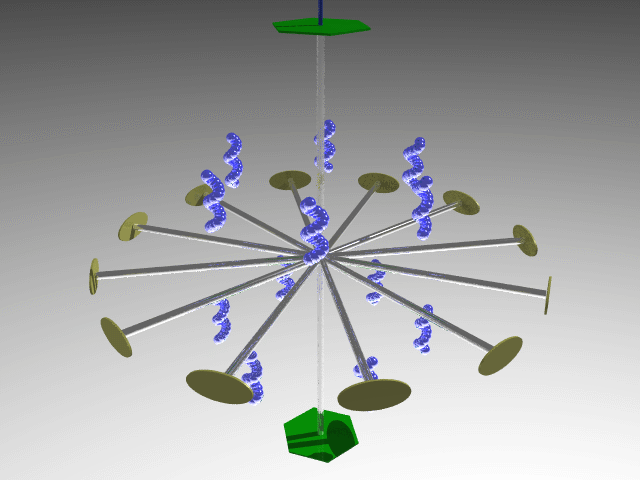

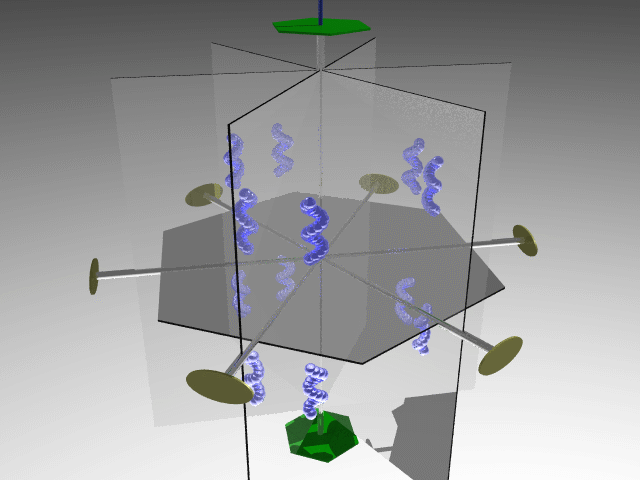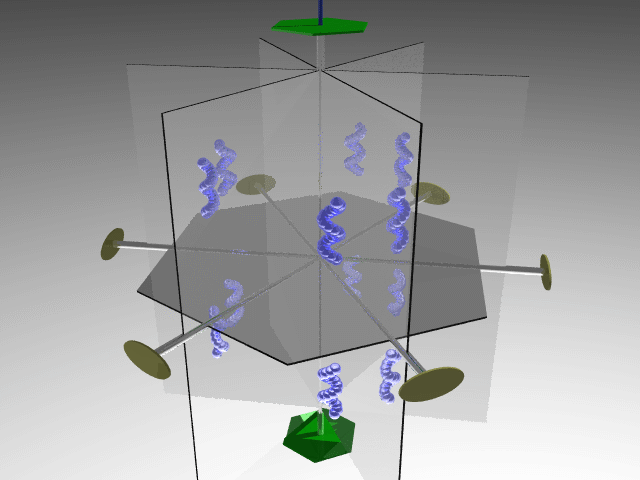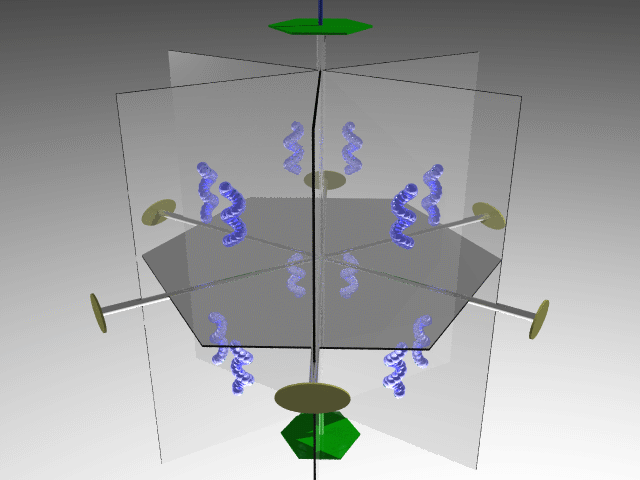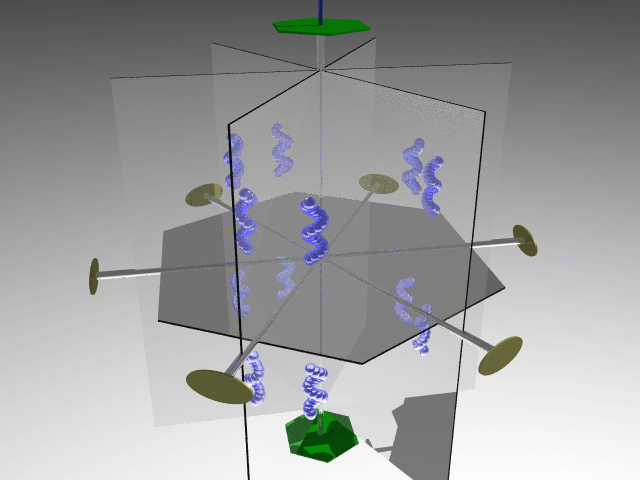
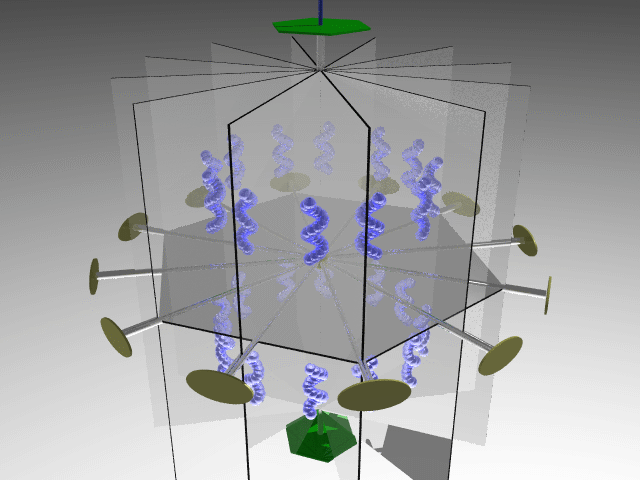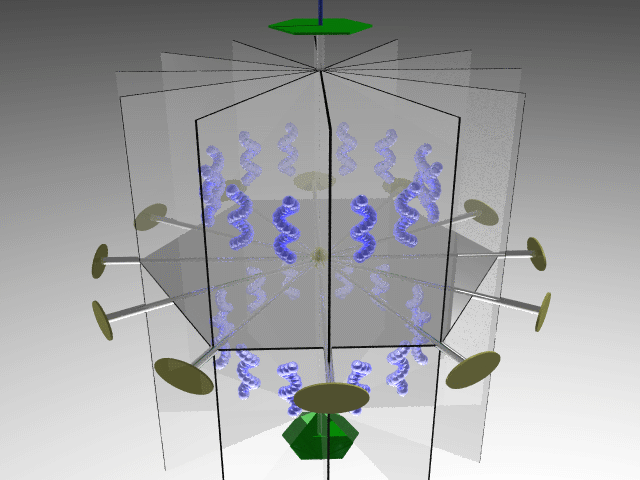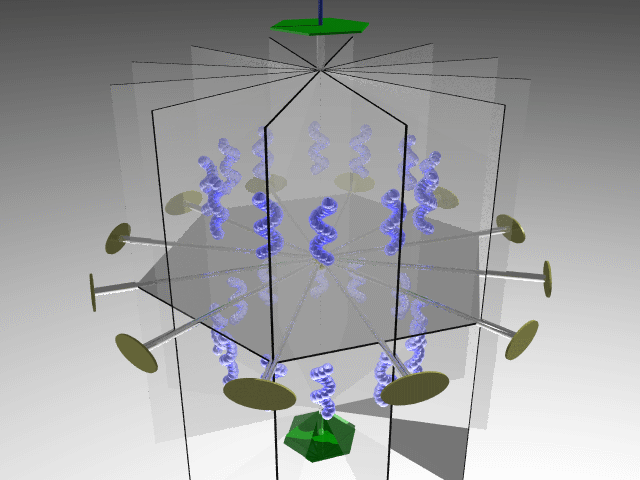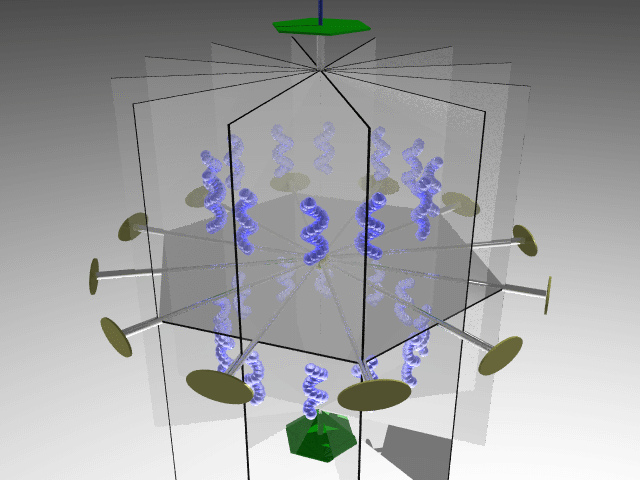
Combining four threefold axes along the cube diagonals generates three twofold axes along the cube's principal axes. The symmetry operators associated with these elements define the 23 point group.
If the four third-order axes are improper, they generate three planes orthogonal to the cube’s principal axes, which, due to the presence of an inversion center, also contain three twofold axes. The symmetry operators associated with these elements define the m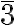 point group.
point group.
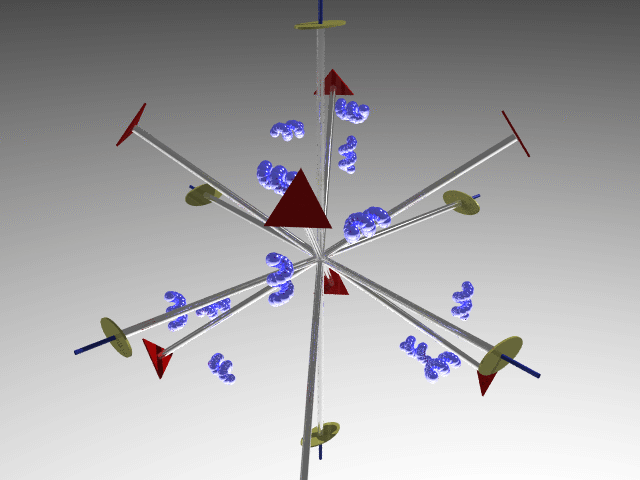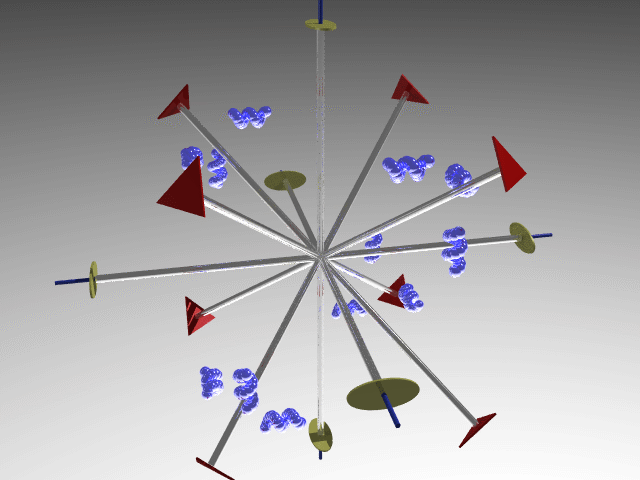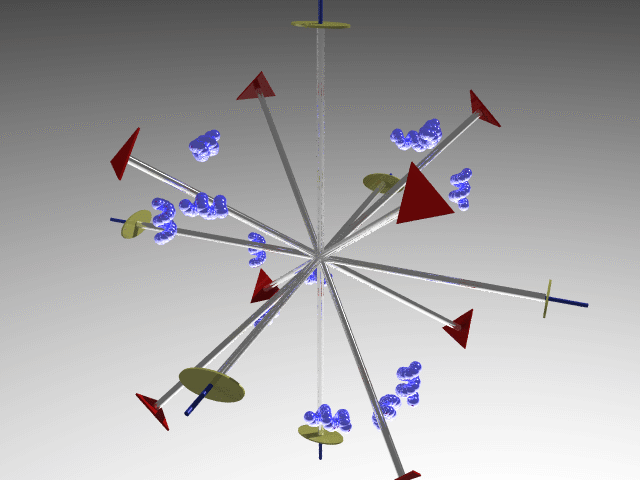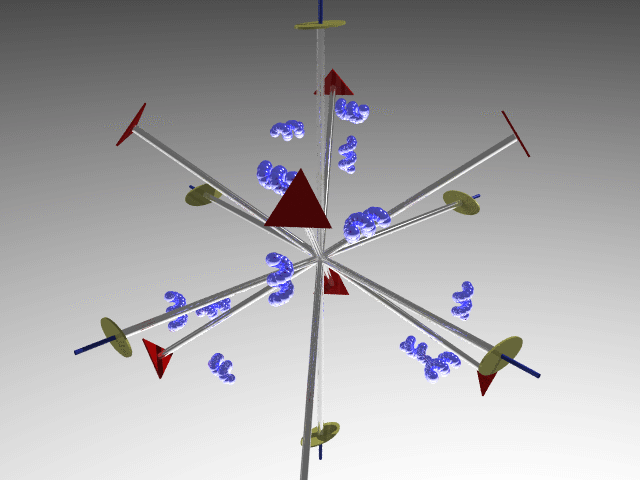
If, in addition to the four third-order axes along the cube's diagonals, three fourfold axes are placed along the cube's principal axes, these axes generating six additional twofold axes located between the threefold axes, then the resulting symmetry defines the 432 point group.
If, instead, three improper fourth-order axes 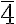 are placed along the cube’s principal axes, generating six symmetry planes, the
are placed along the cube’s principal axes, generating six symmetry planes, the 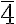 3m point group is obtained.
3m point group is obtained.
If, to the four improper third-order axes along the cube’s diagonals, three fourfold axes with orthogonal planes 4/m along the cube’s principal axes are added, axes that also generate symmetry planes and twofold axes, then the resulting symmetry defines the m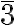 m point group.
m point group.
These five classes, three non-centrosymmetric and two centrosymmetric, belong to the
Cubic system:




Among the 21 non-centrosymmetric classes, the 11 classes that do not contain improper symmetry operations are called enantiomorphic classes. The 11 enantiomorphic classes are:
1, 2, 222, 3, 32, 4, 422, 6, 622, 23, 432.
A class is called polar if it has a polar direction (i.e., the two opposite directions along a given axis are not equivalent by symmetry). The 10 polar classes are:
1, 2, m, mm2, 4, 4mm, 6, 6mm, 3, 3m.
Symmetry Classes and Physical Properties
The symmetry of the physical properties of a crystal is linked to its point group.
A crystal is inherently an anisotropic object, meaning that different directions within the crystal are not equivalent.
Most physical properties are defined by mathematical relations (tensorial relations) that couple two or more measurable quantities.
Many physical quantities are scalar (zero-rank tensor, 30= one scalar value in 3D space), such as temperature, mass, or density, which are not affected by direction within the crystal and are therefore isotropic (e.g., density = mass of the crystal/volume of the crystal)
Other physical properties are vectorial or tensorial quantities, such as force, electric field, and electric polarization, which are vectorial properties (first-rank tensors, 31 = 3 scalar values in the 3D space), as well as pyroelectricity, which involves a vectorial polarization response to temperature changes. Electrical and thermal conductivity are matrix relationships (second-rank tensors, 32 = 3x3 matrix in the 3D space), while piezoelectricity involves a third-rank tensor (33 = tensor with three indices in the 3D space) that relates mechanical stress (a second-rank tensor) to electric polarization (a first-rank tensor). These physical properties depend on the direction of the applied force to crystallographic axes, leading to anisotropic behavior in crystals.
Neumann’s Principle (Symmetry Principle)
Neumann’s principle states that if a crystal is invariant under certain symmetry operations, then its physical properties must also remain invariant under those same symmetry operations. In other words, the symmetry operations of any physical property of a crystal must include the symmetry operations of the point group of the crystal.
According to this principle, the physical properties of a crystal can exhibit equal or higher symmetry than its point group, but never a lower symmetry.
Measurements and analysis of certain physical properties can help to determine a crystal’s point group. Examples include morphological appearance, X-ray diffraction, polarized light rotation, birefringence, piezoelectric properties, etc.
Crystal Morphology
Crystals exhibit a morphology (habit) that reflects the symmetry with which atoms are arranged within the crystal structure.

The morphological appearance therefore reflects the symmetry of the crystal's point group.
For example, NaCl crystals tend to adopt cubic, cuboctahedral, or octahedral habits, which are characteristic of the point group m m,
m,


Meanwhile, sucrose crystals tend to adopt a low-symmetry habit, with some faces meeting along an edge perpendicular to a twofold axis. This forms the basic wedge shape of a sphenoid, which has only one twofold symmetry axis, a characteristic symmetry of the point group 2
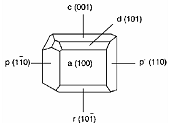
The crystal morphologies differ in the types of faces present, their extent, and the number of edges (although the dihedral angles between corresponding faces remain constant, which is the law of the constancy of interfacial angles, also called the 'first law of crystallography'). These variations depend on the kinetic aspects of crystal growth (see the cuboctahedron example).
However, the overall arrangement of these faces tends to reflect the symmetry of the point group of the crystalline substance, regardless of the morphological habit.
Therefore, the morphological analysis of a crystalline sample is often used to obtain preliminary information about the crystal's point symmetry group.
Piezoelectric Phenomenon
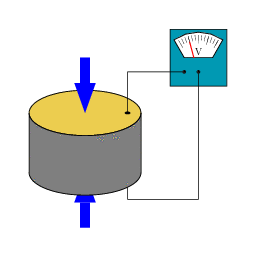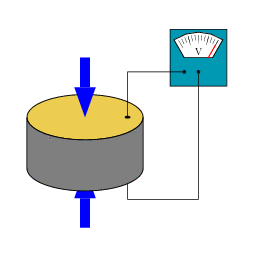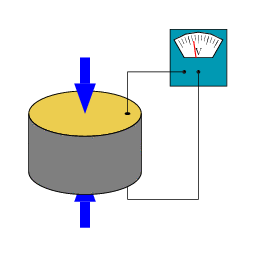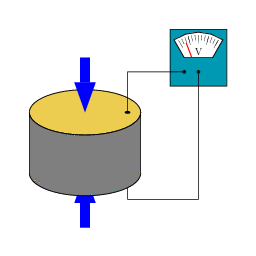
The piezoelectric effect is a phenomenon in which certain crystals develop an electric charge separation, with opposite charges appearing at the two ends of a given direction when subjected to mechanical stress, such as pressure.
The piezoelectric effect can be direct, where mechanical pressure induces an electric field, or inverse, where the application of an electric field causes the crystal elongation.
This effect is observed only in crystals belonging to the 20 non-centrosymmetric classes (excluding, by more elaborated symmetry considerations, the 21th non-centrosymmetric class 432).
However, not all directions in crystals belonging to these 20 classes exhibit the phenomenon. Directions perpendicular to a twofold rotation axis or a mirror plane are not piezoelectric.
For example, in alpha quartz (SiO₂, polar crystal class 32), opposite charges can appear at the ends of the twofold axes, but not at the ends of the direction orthogonal to these axes, which coincides with the crystal’s threefold axis.
The piezoelectric phenomenon has various technological applications, including amplifiers, microphones, electronic components, quartz balances and watches, and nanometric control of mechanical movements.
Pyroelectric Phenomenon
Crystals with polar axes, and therefore belong to the 10 polar classes, can exhibit the pyroelectric phenomenon. Along these directions, a permanent electric dipole is formed within the crystal, which varies when the crystal's temperature changes. When heated, the dipole aligns in a certain direction, whereas when cooled, the dipole reverses.
All crystals that exhibit the pyroelectric phenomenon also exhibit the piezoelectric phenomenon. However, the reverse is not true.
This distinction can be understood by considering that temperature is an isotropic quantity, meaning that, it affects the crystal uniformly in all directions. As a result, an electric dipole is generated only along the polar directions of the crystal. In contrast, applying pressure along a specific crystal direction is inherently anisotropic force, which can alter the symmetry and polarity of the crystal, unless the crystal is centrosymmetric, in which case no piezoelectric effect occurs.
Example: Triglycine sulfate (point group 2)
These crystals are pyroelectric which allows their use as photodetector elements in infrared spectroscopy and night vision applications.
Rotation of Polarized Light
The symmetry of a crystal containing only one enantiomer of an optically active molecule must belong to one of the 11 enantiomorphic point groups.
Crystals belonging to enantiomorphic point groups (even if not composed of chiral molecules) are optically active and will rotate polarized light.
Laue Classes and Diffraction
According to Neumann's principle, many physical phenomena, including X-ray diffraction (excluding the weak anomalous scattering of different species), do not typically reveal the true symmetry of the crystal. Instead, they generally exhibit a higher symmetry. The higher symmetry is obtained by adding a center of inversion to the symmetry elements present in the crystal. This occurs when measurable quantities depend on interatomic vectors rather than atomic positions. In fact, interatomic vectors appear in both directions (for an interatomic vector x,y,z, there is also a corresponding vector with the opposite direction −x,−y,−z), thus forming an overall centrosymmetric set.
Therefore, point groups that differ only by the presence of an inversion center can appear indistinguishable in the diffraction pattern (excluding the weak anomalous scattering). These groups collectively form the 11 centrosymmetric Laue classes. Generally, from X-ray diffraction, it is possible to determine only the Laue class of the crystal, not the point group.
However, if the crystal contains chemical species with significantly different anomalous scattering, the crystal's point group can be determined by analyzing the small differences in diffraction intensity between centrosymmetric pairs (for example, using data from a highly brilliant source, such as synchrotron radiation). Therefore, with anomalous contributions, there is a one-to-one relationship between a crystal's point symmetry and the point symmetry of the diffraction.
