Translational Symmetry in Crystals
Translational symmetry operations in crystals
In crystals, not only point symmetry elements related to proper and improper axes of order 1, 2, 3, 4, and 6 are present, but other symmetry operators can also exist, which combine these point symmetry elements with fractional translations within the unit cell.
Thus, translational symmetry in crystals goes beyond simple lattice translations, and these composite operations are fundamental to describing the full symmetry of crystalline structures.
| Direct congruence | Indirect congruence |
|---|---|
 |
 |
| Roto-translation | Roto-inversion-translation |
| Screw axes | Glide planes |
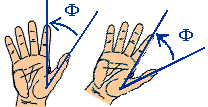
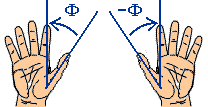
| compatible with all molecules, including enantiopure chiral molecules |
compatible with achiral molecules and racemic mixtures non-compatible with enantiopure chiral molecules |
Rototranslation axes compatible with the crystal lattice
Screw axis 21
There is only one rototranslation axis of order 2 compatible with the crystal lattice.
The translation is along the rotation axis and is equal to half of the unit cell.
If the rototranslation axis is along the y-axis, the point with coordinates x, y, z has its symmetry-equivalent point at -x, 1/2 + y, -z.
In matrix form:
|x’| |-1 0 0| |x| | 0 |
|y’| = | 0 1 0| |y|+|1/2|
|z’| | 0 0 -1| |z| | 0 |
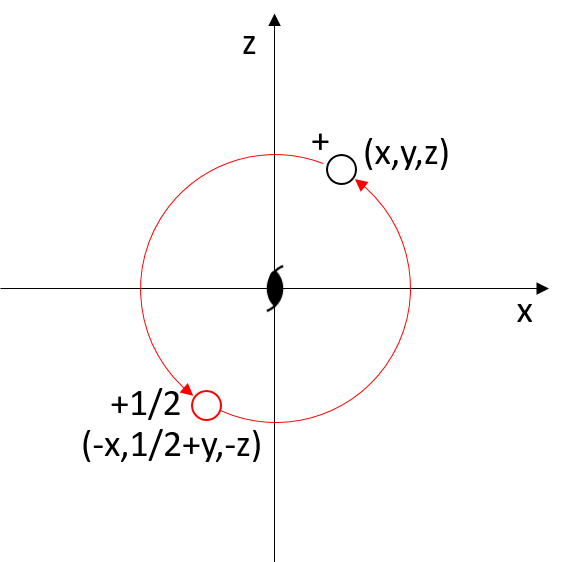
Applying the twofold rototranslation operation twice results in an equivalent point by translation of one unit cell along the rotation axis.
Symbols used in symmetry descriptions in the International Tables for Crystallography
For a roto-translation axis of order 2,
orthogonal and parallel to the sheet

Screw axes 31 and 32
There are 2 rototranslation axes of order 3 compatible with the crystal lattice.
The translations along the rotation axis are equal to 1/3 or 2/3 of the unit cell.
These two screw axes, 31 and 32, are enantiomorphic.
If the 31 rototranslation axis is along the z-axis, and a hexagonal coordinate system is used (with an angle γ between the x and y axes = 120°), the point with coordinates x, y, z has its first symmetry-equivalent point at -y, x - y, 1/3 + z.
In matrix form:
|x’| | 0 -1 0| |x| | 0 |
|y’| = | 1 -1 0| |y| + | 0 |
|z’| | 0 0 1| |z| |1/3|
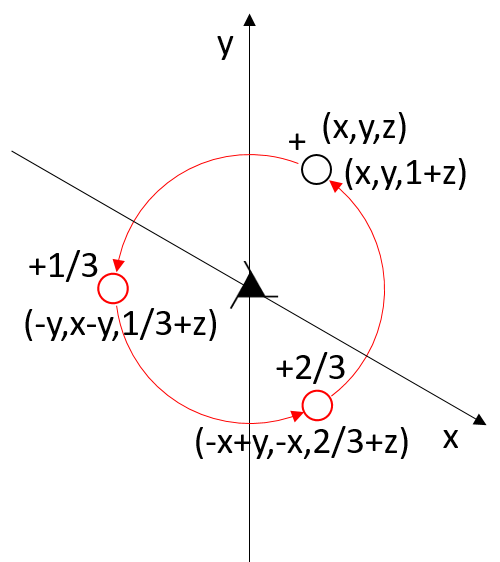
Applying the rototranslation operation of order 3 three times results in an equivalent point by one unit cell translation along the rotation axis.
Relation between the symmetry-equivalent points of the screw axis 32, which is enantiomorphic to 31
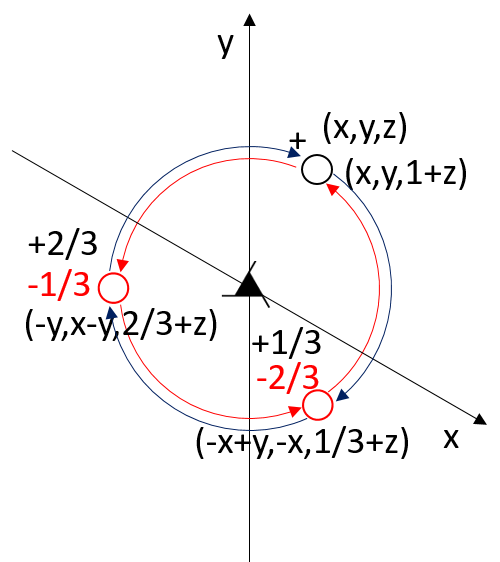
Symbols used in the description of symmetry in the International Tables for Crystallography
The two roto-translation axes 31 and 32,
orthogonal to the plane and along the diagonals of a cube.
Screw axes 41, 42 e 43
There are 3 rototranslation axes of order 4 compatible with the crystal lattice.
The translations along the rotation axis are equal to 1/4, 2/4 (1/2), or 3/4 of the unit cell.
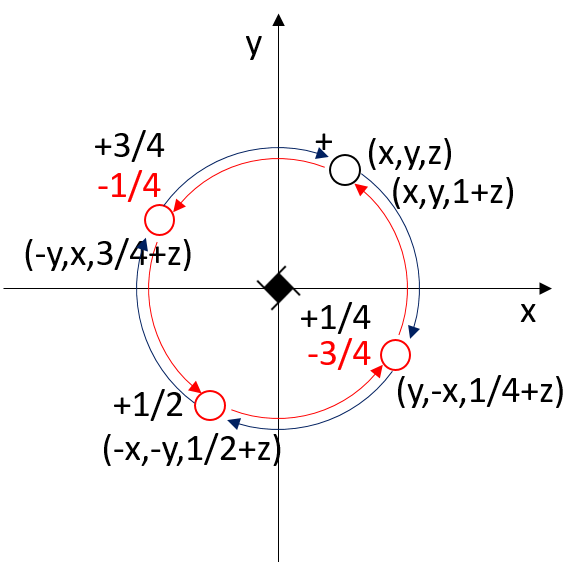
The screw axes 41 and 43 are enantiomorphic.
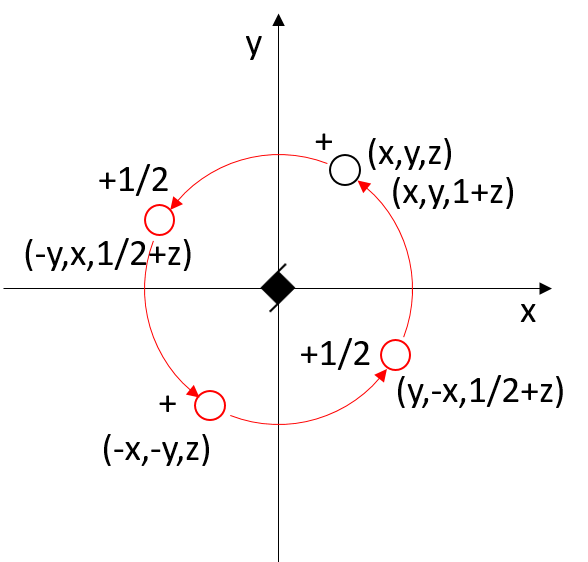
The axis 42 also has a twofold axis that coincides with the screw axis.
If the rototranslation axis 41 is along the z-axis, the point with coordinates x, y, z has its first symmetry-equivalent point at -y, x, 1/4 + z.
In matrix form:
Ci sono 3 asse di roto-traslazione di ordine 4 compatibile con il reticolo cristallino.
|x’| | 0 -1 0| |x| | 0 |
|y’| = | 1 0 0| |y| + | 0 |
|z’| | 0 0 1| |z| |1/4|
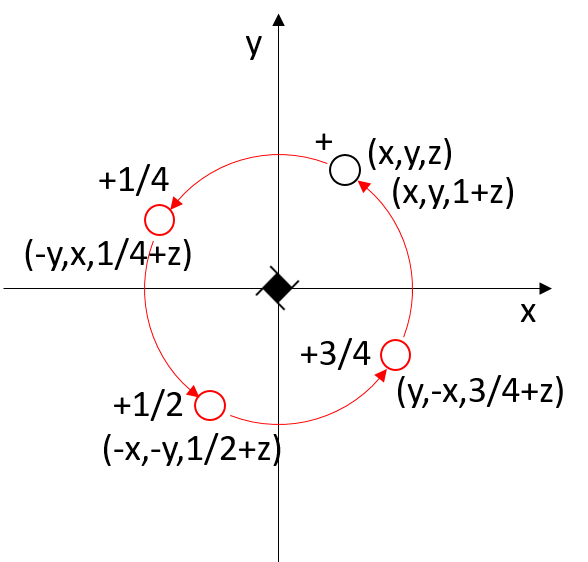
Applying the rototranslation operation of order 4 four times results in an equivalent point by one unit cell translation along the rotation axis.
Relation between the symmetry-equivalent points of the screw axis 42, which also coincides with a twofold axis.
Relation between the symmetry-equivalent points of the screw axis 43, which is enantiomorphic to 41.
Symbols used in the description of symmetry in the International Tables for Crystallography
The three roto-translation axes 41, 42, and 43,
orthogonal and parallel to the plane

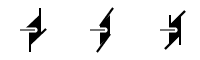
Screw axes 61, 62, 63, 64 e 65
There are 5 rototranslation axes of order 6 compatible with the crystal lattice.
The translations along the rotation axis are equal to 1/6, 2/6 (1/3), 3/6 (1/2), 4/6 (2/3), or 5/6 of the unit cell.
The two pairs of screw axes 61 65 and 62 64 are enantiomorphic.
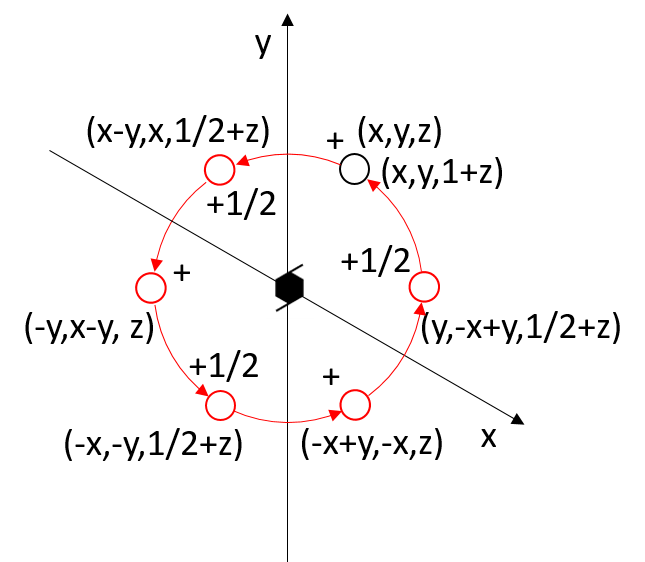
The 62 and 64 axes also have a twofold axis that coincides with the screw axis.
The 63 axis has a threefold axis that coincides with the screw axis.
If the 61 rototranslation axis is along the z-axis,
the point with coordinates x, y, z has its first symmetry-equivalent point at x - y, x, 1/6 + z.
In matrix form:
|x’| | 1 -1 0| |x| | 0 |
|y’| = | 1 0 0| |y| + | 0 |
|z’| | 0 0 1| |z| |1/6|
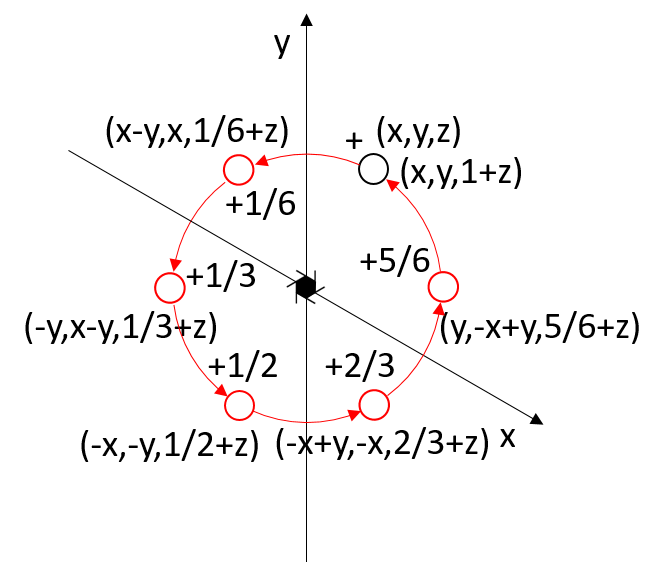
Applying the roto-translation operation of order 6 six times results in an equivalent point by one unit cell translation along the rotation axis.
Relation between the symmetry-equivalent points of the screw axis 62, which also coincides with an axis of order 2
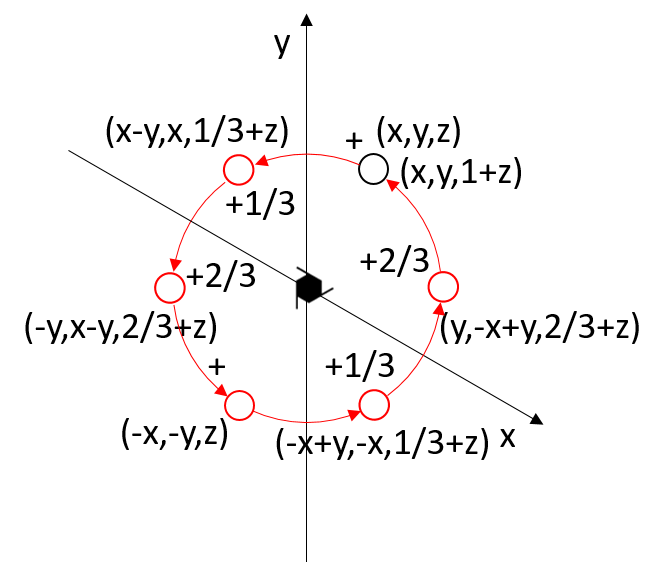
Relation between the symmetry-equivalent points of the screw axis 63, which also coincides with an axis of order 3
Relation between the symmetry-equivalent points of the screw axis 64, which is enantiomorphic to 62
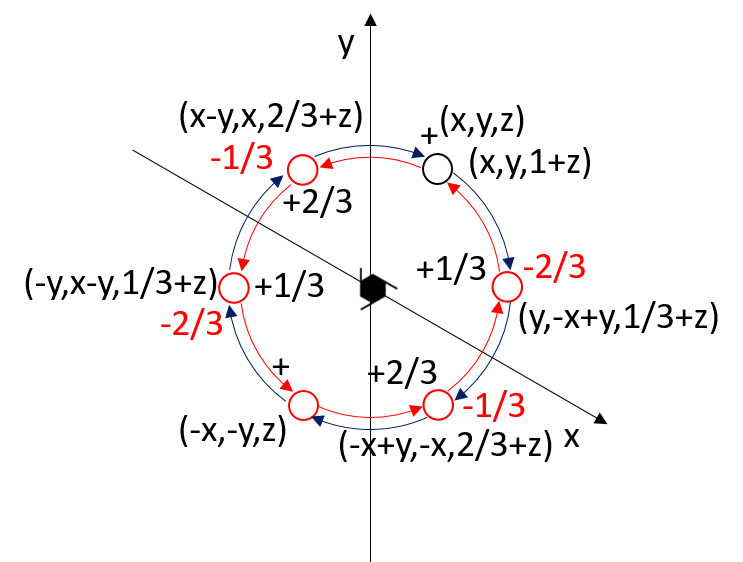
Relation between the symmetry-equivalent points of the screw axis 65, which is enantiomorphic to 61.
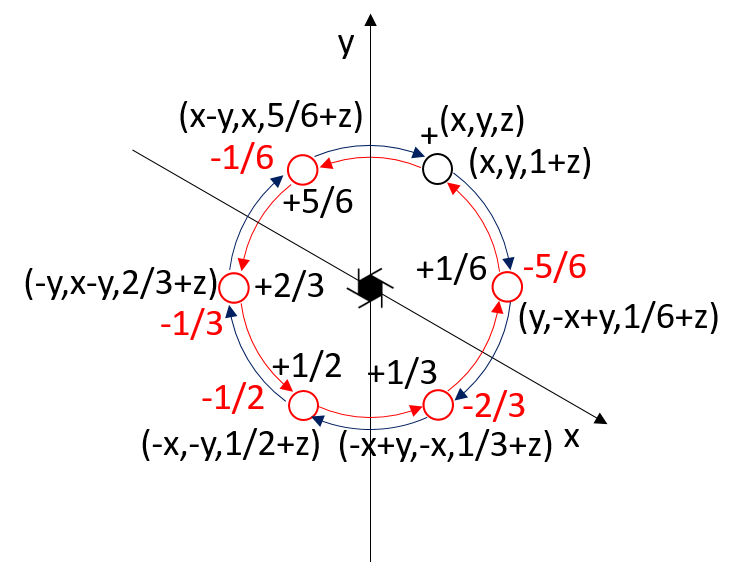
Symbols used in the description of symmetry in the International Tables for Crystallography
The five roto-translation axes 61, 62, 63, 64, and 65,
orthogonal to the plane.

Planes with translation (Glide planes)
The improper axis of roto-inversion of order 2 (mirror plane) can be combined with a translation to generate a glide plane.
The translation is parallel to the mirror plane, and the magnitude of the translation is generally 1/2 along an axis or a diagonal of the unit cell. In this way, the double application of the glide plane is compatible with the crystal lattice because it translates the points of one unit cell into the next unit cell.
The glide plane symmetry element can be of type a, b, or c (axial glide plane) if the translation is along one of these three axes, with the mirror plane parallel to the same axis; or it can be of type e (double glide plane) if translations are present along both axes parallel to the reflection plane; or of type n (diagonal glide plane) if the translation is 1/2 along the diagonal of the two axes parallel to the mirror plane; or of type d (diamond glide plane) when the translation is 1/4 along the diagonal.
For example, for the glide plane a, which contains the a and b axes and is orthogonal to the c axis, the generic point with coordinates x, y, z has its symmetry-equivalent point at 1/2 + x, y, -z.
In matrix form
|x’| | 1 0 0| |x| |1/2|
|y’| = | 0 1 0| |y| + | 0 |
|z’| | 0 0 -1| |z| | 0 |
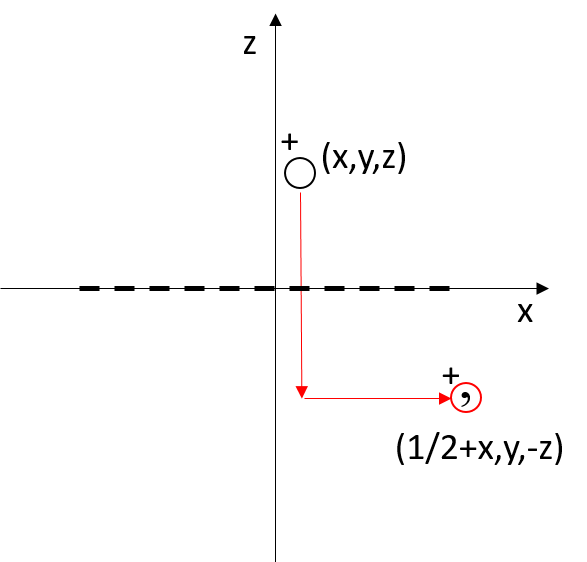
Applying the reflection operation with translation twice results in translating the points of a unit cell along the direction of the a axis.
The symbols used in the description of symmetry in the International Tables for Crystallography
for the axial glide planes a, b, and c,
with the glide plane parallel to the sheet, the arrows indicate the direction of the translation
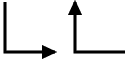
with the glide plane perpendicular to the plane, the dashed line indicates a translation in the direction of the line, thus parallel to the plane, while the dotted line indicates a translation orthogonal to the direction of the line and parallel to the plane.
![]()
In the case of the double glide plane e, where there are two translations along both directions of the unit cell, the symbols used for glide planes parallel and orthogonal to the plane are:
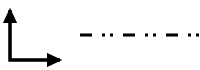
For the diagonal glide plane n with a translation of 1/2 along the face diagonal of the unit cell, parallel or orthogonal to the plane

For the diamond, d glide plane with a translation of 1/4 of the face diagonal of the unit cell, arranged parallel or orthogonal to the plane

