Relationship between Symmetry and Crystal Lattice
Constraints imposed on cell parameters by symmetry elements
The presence of specific symmetry elements that relate atoms in a crystal imposes certain constraints on the geometric parameters of the unit cell.
2-fold axis (Proper, improper with or without translation)
The 2-fold axis imposes two 90° angles with the other two axes.
If only 1-fold axes (identity) are present along the other two directions of the unit cell, the axis containing the 2-fold axis is called the unique axis and, by convention, corresponds to the b axis of the unit cell. Consequently, the angles that take values of 90° are α and γ.
If additional 2-fold axes are orthogonally present, all three angles, including β, must assume 90° values.
4-fold axis (proper, improper with or without translation)
The 4-fold axis generates an orthogonal unit cell with two equal axes.
By convention, the 4-fold axis corresponds to the c axis of the unit cell. Consequently, the a and b axes are equal, and all unit cell angles are 90°.
3- and 6-fold axes (proper, improper with or without translation)
The 3-fold or 6-fold axes generate hexagonal unit cells, which have a 120° angle between the two equal axes perpendicular to the axis with 3-fold or 6-fold symmetry.
By convention, the 3-fold or 6-fold axis corresponds to the c axis of the unit cell. Consequently, the angle γ between the two equal axes a and b is 120°, while the angles α and β are 90°.
Cubic unit cells, with all equal axes and angles of 90°, arise from the presence of four 3-fold symmetry axes aligned along the cube's diagonals.
Crystal Families and Crystal Systems
Crystals can be classified into six distinct Crystal Families and/or seven distinct Crystal Systems, based on the presence of specific symmetry axes (proper and improper, with or without translation), which impose certain constraints on the unit cell parameters.
The two classifications are almost identical; however, while the Crystal System emphasizes the symmetry that generates these geometric constraints, the Crystal Family focuses on the constraints on the unit cell parameters.
Therefore, the Crystal Families and Crystal Systems coincide, except for the Trigonal System, which imposes the same unit cell constraints as the Hexagonal System. In this case, there is only one family: the Hexagonal Family.
| Symmetry axes | Family- System | Constraints on the unit cell |
|---|---|---|
| order 1 | Triclinic - Triclinic | nessuno |
| order 2 | Monoclinic - Monoclinic | α=γ=90° |
| order 2 orthogonal | Orthorhombic - Orthorhombic | α=β=γ=90° |
| order 3 | Hexagonal - Trigonal | a=b α=β=90° γ=120° |
| order 6 | Hexagonal - Hexagonal | a=b α=β=90° γ=120° |
| order 4 | Tetragonal - Tetragonal | a=b α=β=γ=90° |
| order 3 diagonal | Cubic - Cubic | a=b=c α=β=γ=90° |
Crystal lattice and unit cell
Given a lattice, an infinite number of unit cells can reconstruct the lattice through translation.
Unit cell
The Unit Cell is the parallelepiped constructed from the axes a, b, and c, which axes identify three non-coplanar vectors of the lattice.
Reduced Cell
Given a crystal lattice, there is a unique right-handed unit cell with the following characteristics:
-
The a axis is the shortest vector among the vectors defined by the lattice nodes.
-
Excluding collinear vectors to a, the b axis is the shortest vector.
-
Excluding coplanar vectors to a and b, the c axis is the shortest vector.
-
The α, β, and γ are all acute angles (Reduced cell of the first type).
-
Alternatively, α, β, and γ are all obtuse angles (Reduced cell of the second type).
Given a lattice, there is only one reduced unit cell, although, depending on the symmetries, various orientations of the reduced cell may be present.
Centered Cell
A Centered Cell contains more than one lattice node within the cell.
Conventional Cell
The conventional cell has the following characteristics:
-
Its base vectors define a right-handed coordinate system;
-
Its cell edges are aligned with the symmetry directions of the lattice;
-
It is the cell with the smallest volume compatible with the above conditions.
Crystals with the same type of conventional cell belong to the same crystal family
Need to introduce centered cells and lattices when symmetry elements are not along the axes of the reduced cell.
Bravais Cells (Lattices)
Primitive or centered cells with cell edges along the symmetry directions are called Bravais Cells.
Bravais cells generate, through translation, the corresponding Bravais lattices, which are characterized by a symmetric arrangement of nodes that reflects the symmetry of the corresponding crystal family.
There are a total of 14 different Bravais lattices, generated by the corresponding Bravais cells (primitive or centered), compatible with the symmetry of one of the 6 different crystal families.
Triclinic Family
The absence of rotation axes of order 2 or higher also implies the absence of constraints on the unit cell parameters.
The simple cell conventionally adopted for the triclinic (anorthic) system is the reduced primitive cell. The three axes of the right-handed system, shown in the figures below, are represented with the following colors: a = red, b = green, c = blue.
aP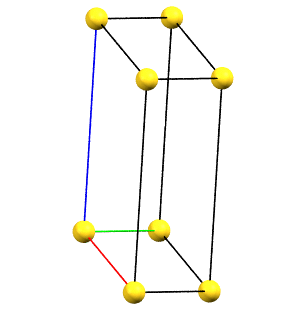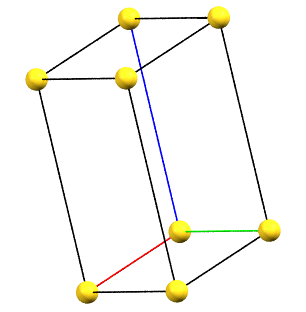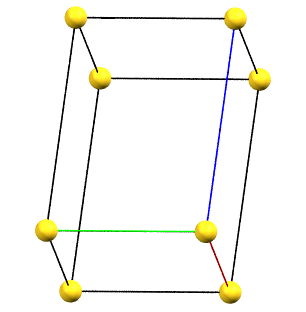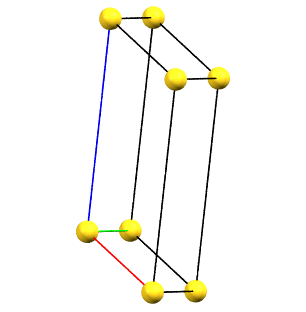
Monoclinic Family
The presence of rotation axes of order 2, either proper or improper (planes of symmetry orthogonal to the improper axis), along a single direction (unique axis), implies the presence of a geometric constraint of 90° for two angles of the unit cell.
If the direction of the 2-fold symmetry coincides with one of the three axes of the reduced cell, by convention, this direction (unique axis) is assigned to the b axis, regardless of the axis length. In this case, a primitive cell is used with a < c, geometric constraints α = γ = 90°, and the angle β > 90° being as small as possible.
mP
In the monoclinic system, if the 2-fold symmetry axes are along a diagonal of the reduced cell, a C-centered cell (with the ab face and a translation operation of 1/2, 1/2, 0) is used by convention, with the b axis as the unique axis and therefore with the geometric constraints α = γ = 90°. The face-centered cell has double the volume of the primitive cell.
mC 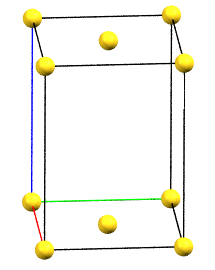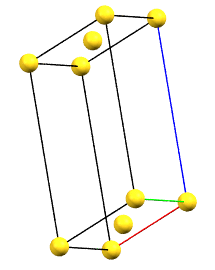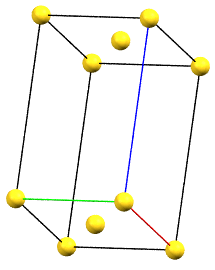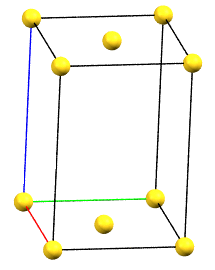
Orthorhombic Family
In the orthorhombic family, there can be as many as four different Bravais cells, which differ in the direction of the orthogonal axes of order 2 (either proper or improper) compared to the reduced cell.
If the directions of the reduced cell and the order 2 symmetries coincide, the cell, by convention, will be a primitive cell with angles α = β = γ = 90°. If the three directions are all equivalent by symmetry, the order of the axes will conventionally reflect the axes lengths themselves (a < b < c). However, if the directions are not equivalent, the order will be determined by the symmetry of the reference standard space group. For example, a crystal of class mm2 has two equivalent directions (improper 2-fold axes, mirror planes m) and one direction with 2-fold axes. The c axis will therefore be defined by the two-fold axes direction, while the a and b axes will follow the metric order.
oP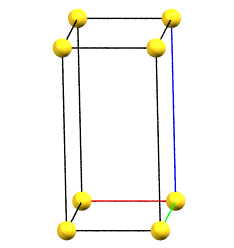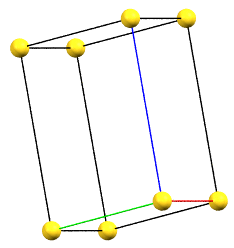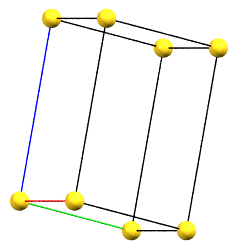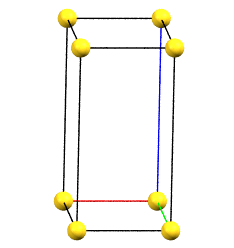
When one of the axes of the reduced cell does not coincide with one of the three orthogonal directions with two-fold symmetry, and this axis develops diagonally relative to two of the directions with orthogonal two-fold axes, a face-centered orthorhombic Bravais cell will result. By convention, the face-centered cell is either the C face (the ab face with node translation at 1/2, 1/2, 0) or the A face (the bc face with node translation at 0, 1/2, 1/2), both with cell angles α = β = γ = 90°. The A or C centering depends on the choice of the a, b, and c axes, which by convention is defined by the symmetry of the standard space group. The face-centered cell has double the volume of the primitive cell.
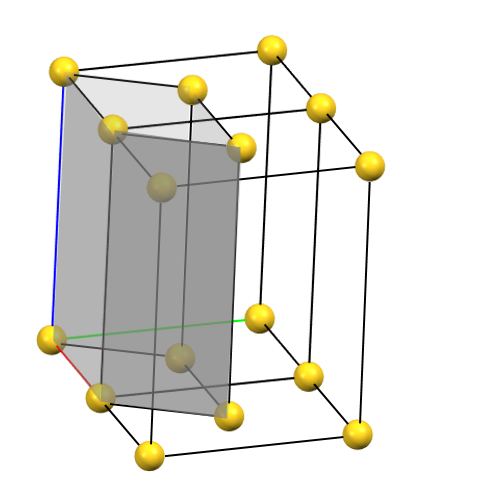
oC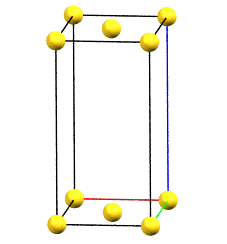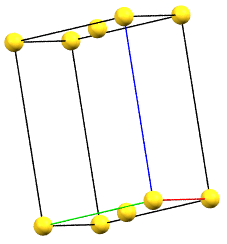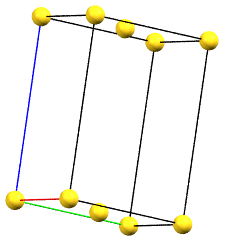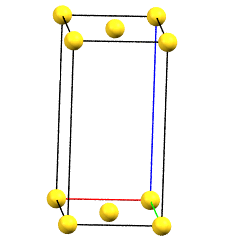
When one of the axes of the reduced cell does not coincide with one of the three orthogonal directions with two-fold symmetry, and this axis develops diagonally relative to all three directions of the two-fold axes, a body-centered orthorhombic Bravais cell I (from the German Innerzentrierte with translation 1/2, 1/2, 1/2) will result, with angles α = β = γ = 90°. The body-centered cell has double the volume of the primitive cell.
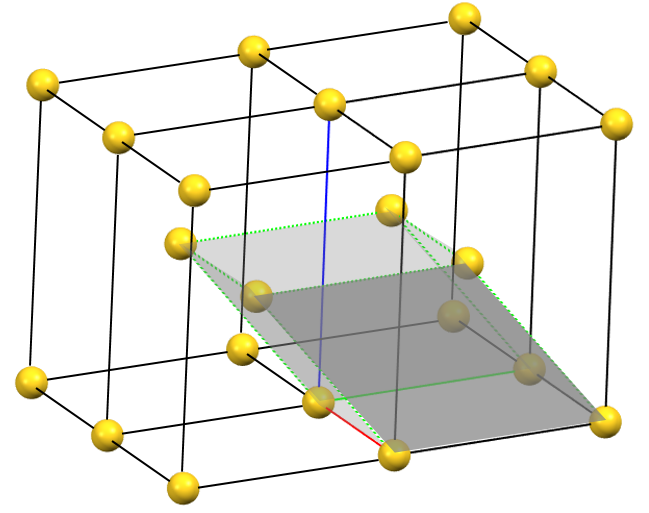
oI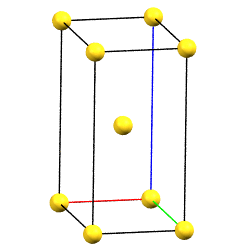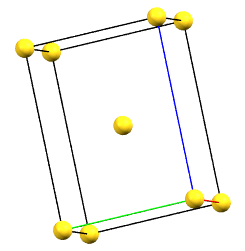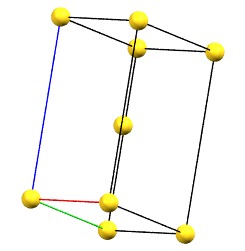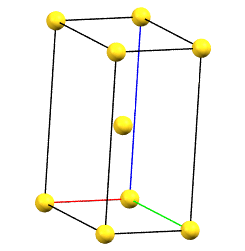
When two of the axes of the reduced cell develop diagonally relative to two faces defined by the two-fold axes, a face-centered orthorhombic Bravais cell F will result (the translations will be 1/2, 1/2, 0; 1/2, 0, 1/2; and 0, 1/2, 1/2), with angles α = β = γ = 90°. The face-centered cell has four times the volume of the primitive cell.
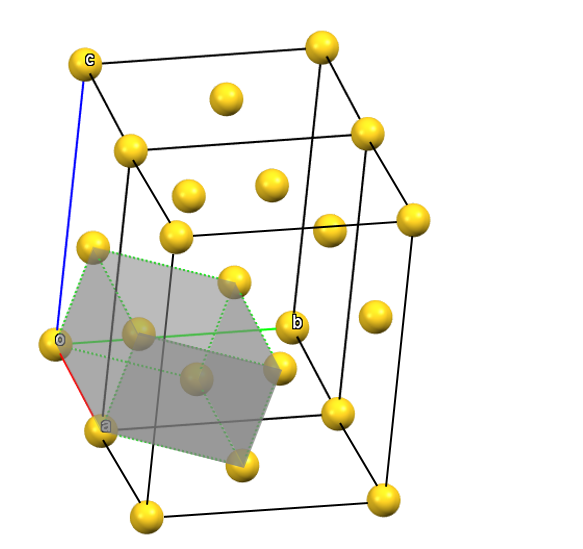
oF
Tetragonal Family
In the tetragonal family, the conventional primitive cell has the c axis aligned with the direction of the 4-fold symmetry axes, while the two a and b axes are equivalent by symmetry and form 90° angles between the axes.
tP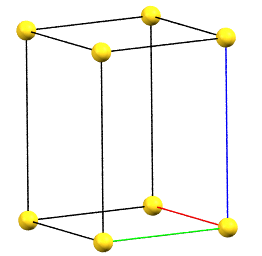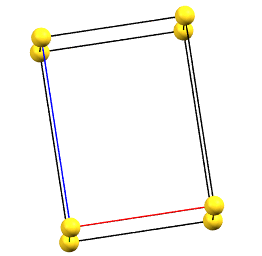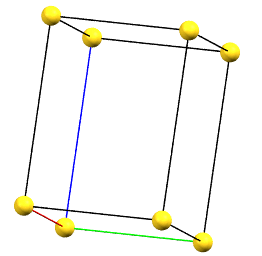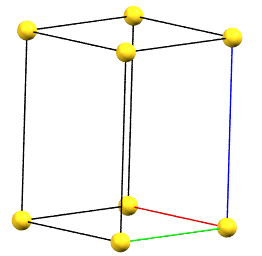
The only tetragonal-centered cell that can occur due to misalignment of the symmetry with the axes of the reduced cell is the body-centered tetragonal cell I.
A face-centered tetragonal cell C can always be reduced to the simpler primitive tetragonal cell, while a cell with a single A or B face-centered is not compatible with the symmetry equivalence of the a and b axes. The face-centered tetragonal cell F can be reduced to a simpler body-centered tetragonal cell I, which is only double in volume compared to the primitive cell.
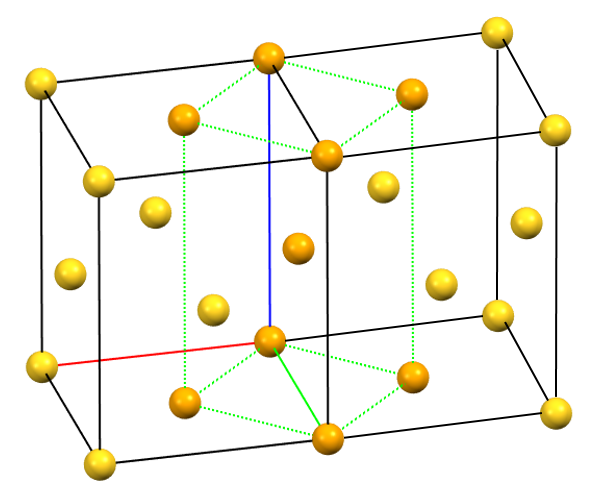
tI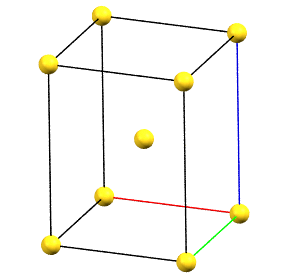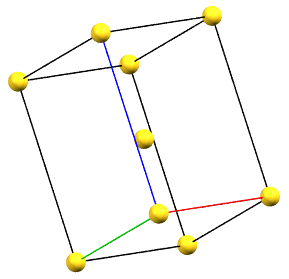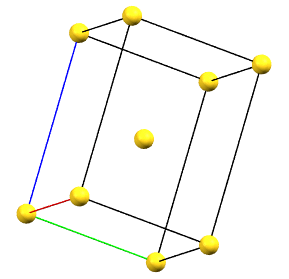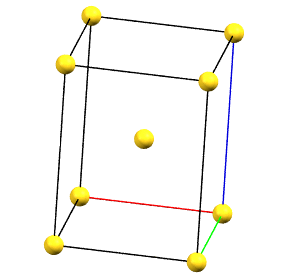
Hexagonal Family
In the hexagonal family, the conventional primitive cell has the c axis aligned with the direction of the 3-fold or 6-fold symmetry axes, while the two a and b axes are equivalent by symmetry and form a 120° angle between each other and a 90° angle with the c axis.
hP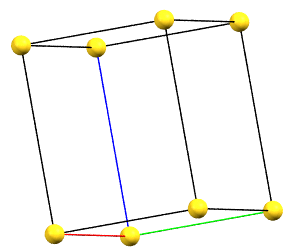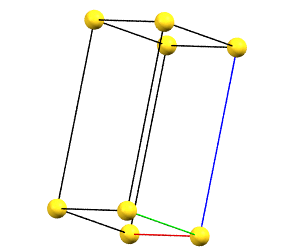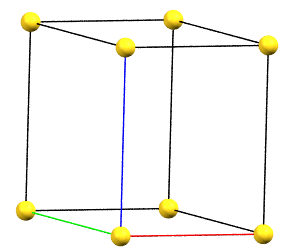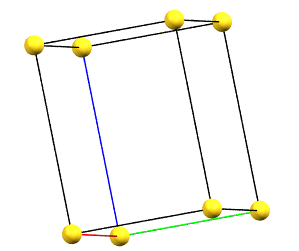
There is only one centering compatible with the hexagonal family, and it is a rhombohedral centering R (translations of 1/3, 2/3, 2/3 and 2/3, 1/3, 1/3 in the hexagonal cell with a = b, α = β = 90°, and γ = 120°), which occurs in some symmetries of the trigonal system. In this case, the centered hexagonal lattice can also be reconstructed from a primitive rhombohedral cell, which has all axes equal (a = b = c) and all angles equal (α = β = γ). The centered hexagonal cell has three times the volume of the primitive rhombohedral cell. The centered hexagonal cell and the rhombohedral cell are equivalent, and both are standard cells. The centered hexagonal cell has the advantage of describing the lattice in terms of a cell with the typical constraints of the hexagonal family. The rhombohedral cell has the advantage of being a simpler representation.
hR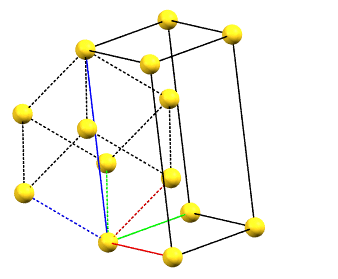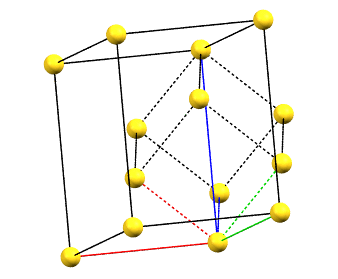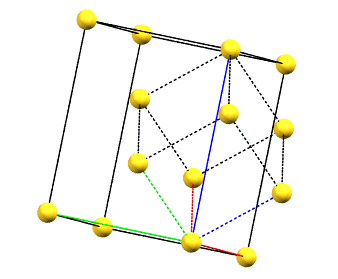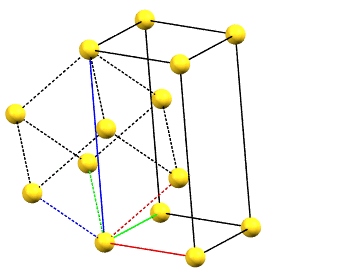
cP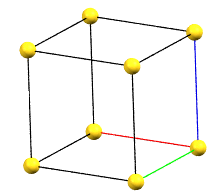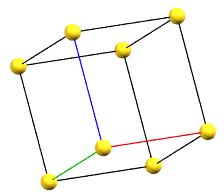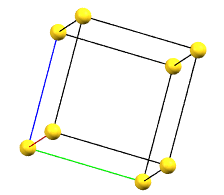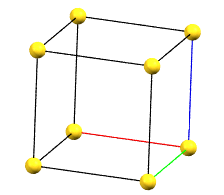
The body-centered cubic cell I has double the volume of the primitive cell..
cI 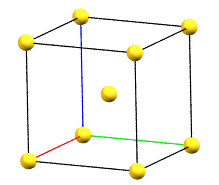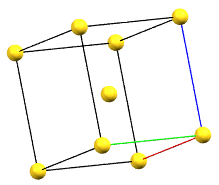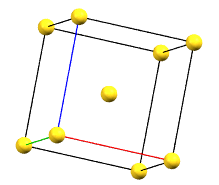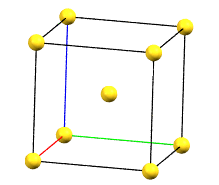
The face-centered cubic cell F has four times the volume of the primitive cell.
cF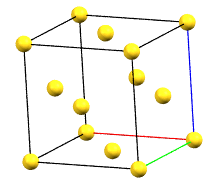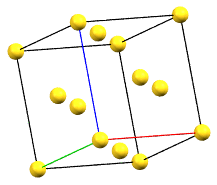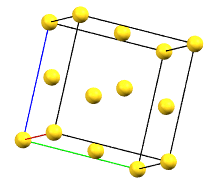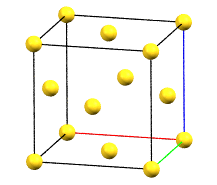
Niggli Matrix
Given the three base vectors a, b, and c of the unit cell, the metric matrix (or metric tensor) G is defined as the symmetric matrix that has as elements the scalar products of the various vectors:
|aa ab ac|
|ba bb bc| = G
|ca cb cc|
The determinant of G is equal to the square of the volume V².
In general, the scalar product of two vectors defined in the cell's metric system (expressed in fractional cell coordinates, also known as crystallographic coordinates) is expressed as:
r1r2 = 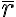 1Gr2= |x1 y1 z1||aa ab ac||x2|
1Gr2= |x1 y1 z1||aa ab ac||x2|
|ba bb bc||y2|
|ca cb cc||z2|
The metric matrix of the reduced cell, defined by Niggli in its compact form, is called the Niggli matrix.
|aa bb cc|
|bc ac ab|
which is equivalent in terms of unit cell parameters.
|a2 b2 c2 |
|bccosα accosβ abcosγ|
From the relationships between the terms of this matrix, one can deduce the Bravais lattices and, therefore, the cells compatible with certain symmetries.
Frequency of Bravais Cells
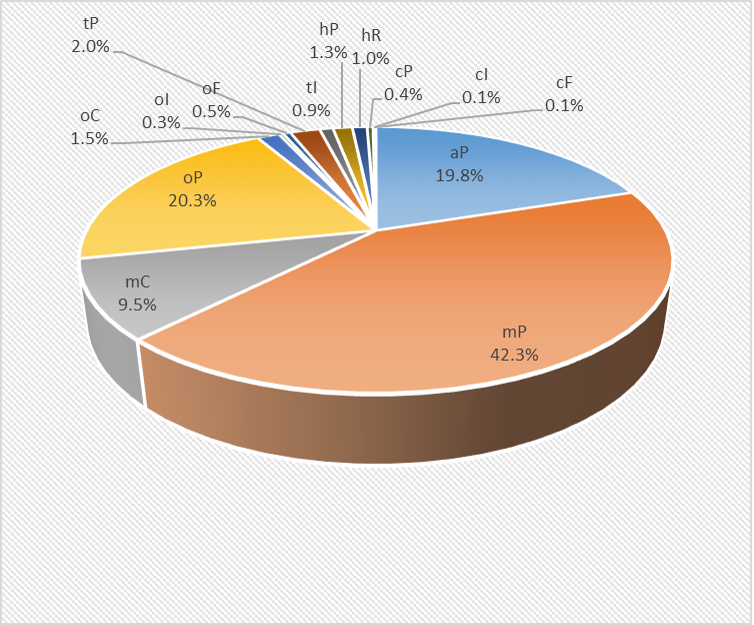
The statistical analysis of crystallographic databases shows an unequal distribution of the frequency of various crystal lattices. In metals, covalent crystals, and inorganic ionic crystals, high-symmetry systems are very common, while in "organic" crystals containing C-C bonds, collected in the CCD (Crystallographic Cambridge Data Base), the frequency of low-symmetry systems is much higher.
|
Cell |
% |
|
|
aP |
19.8 |
|
|
mP |
42.3 |
|
|
mC |
9.5 |
|
|
oP |
20.3 |
|
|
oC |
1.5 |
|
|
oI |
0.3 |
|
|
oF |
0.5 |
|
|
tP |
2.0 |
|
|
tI |
0.9 |
|
|
hP |
1.3 |
|
|
hR |
1.0 |
|
|
cP |
0.4 |
|
|
cI |
0.1 |
|
|
cF |
0.1 |
|