Crystal Symmetry and Space Groups

Space Groups

Just as the combination of point symmetry elements compatible with the crystal lattice generates 32 distinct crystal classes, the combination of all symmetry elements compatible with the lattice—including translational operations (screws and glides) and the 14 Bravais lattices—results in 230 different symmetry groups in 3D space, known as Space Groups.

The 230 Space Groups are compiled in Volume A of the International Tables for Crystallography.

Space Group Symbols

The various space groups are sequentially numbered from 1 to 230, starting with the group of lowest symmetry, P1 (1), and ending with the highest symmetry group, Ia$\bar{3}$d (230). A space group symbol identifies each space group.

According to the Hermann-Mauguin notation, the most relevant conventions followed in space group symbols are:

• The first position contains a capital letter representing the Bravais lattice centering symbol.

• In monoclinic space groups, the Hermann-Mauguin symbol includes the symbol of the twofold symmetry axis (proper or mirror plane m), with or without translational components. If an additional glide or mirror plane is present, normal to this axis, it is indicated after a slash.

• In orthorhombic space groups, the symmetry elements are listed sequentially along the a, b, and c directions.

• In tetragonal space groups, the first symmetry symbol denotes the fourfold axis. If a glide or mirror plane is present, it appears after a slash. The next symbol represents symmetry along the a direction (and therefore also along b by symmetry), followed by the symmetry along the diagonals of the C face.

• In trigonal and hexagonal space groups, the first symmetry symbol represents the threefold or sixfold axis. In hexagonal groups, if a glide or mirror plane is present, normal to this axis, it appears after a slash. The second symbol denotes symmetry along the a axis (and by extension along b and the short diagonal of the C face). The third symbol represents symmetry along the long diagonal of the C face.

• In cubic space groups, the symmetry elements are given in order along the cube edges (axes a, b, c), along the main cell diagonals (where threefold axes occur), and along the face diagonals (A, B, C faces).

Symmorphic Space Groups

Out of the 230 space groups, 73 are symmorphic, meaning they do not contain screw axes or glide planes (e.g., P222, Cmm2, F23). These symmorphic space groups contain special points that retain the same point symmetry as their corresponding crystal class. Conventionally, the cell origin is placed at one of these special points where symmetry operators intersect.

Bieberbach Space Groups

On the other hand, only 13 space groups lack fixed points (no special Wyckoff positions). These groups contain only symmetry elements with translation and are known as Bieberbach or fixed-point-free space groups  (e.g., P2₁).

Arithmetic Crystal Classes

Each 73 symmorphic space groups corresponds to an arithmetic crystal class. The arithmetic crystal class is indicated by placing the lattice symbol at the end  (e.g., 222P, mm2C, 23F). The non-symmorphic space groups belong to the arithmetic crystal class derived by converting translational symmetry elements into their non-translational counterparts. For example, the space group C222₁ belongs to the arithmetic crystal class 222C. 

Enantiomorphic Space Groups

There are 11 enantiomorphic pairs (e.g., P3₁ and P3₂), where if the (+) isomer crystallizes in one space group, the (–) isomer crystallizes in the corresponding enantiomorphic space group.

Sohncke Space Groups

The Sohncke space groups, which do not contain improper symmetry elements (including glide planes), are 65 in total (including the 22 chiral space groups from the 11 enantiomorphic pairs). These are the only space groups compatible with all types of molecules, including enantiopure chiral molecules. The remaining 165 space groups, which contain indirect-congruent symmetry elements, are compatible only with achiral molecules or racemic mixtures.

Relationship Between Space Groups and Point Groups

The point group associated with a given space group can be determined by omitting all translational symmetry elements from the space group symbol.

This means:

• Lattice symbols (including centering) are removed.

• Screw axes are converted into pure rotation axes.

• Glide planes are replaced by mirror planes.

For example, the space groups P4₂/mmc, P4/ncc, and I4₁/acd belong to the same 4/mmm point group.

Frequency of Space Groups in Crystallography

Just as Bravais lattice packing affects the frequency of observed crystal lattices, similar trends are seen for space groups.

In general, symmetry operations with translation (screw axes and glide planes) are more efficient at packing irregularly shaped objects compared to pure rotation or reflection.

For example, in the CCDC (Cambridge Crystallographic Data Centre), the frequency of primitive orthorhombic space groups containing only proper rotation axes increases exponentially with the number of screw axes:

• P222 = 0.1%

• P222₁ = 0.2%

• P2₁2₁2 = 5.0%

• P2₁2₁2₁ = 94.7%

This trend explains the strong asymmetry in space group frequencies. Among organic molecules, the most common space groups are:

• P21/c (35%)

• P$\bar{1}$ (13.3%)

• P2₁2₁2₁ (12.4%)

• P2₁ (7.6%)

• C2/c (6.9%)

Notably, about half of all chiral structures crystallize in the P2₁2₁2₁ space group.

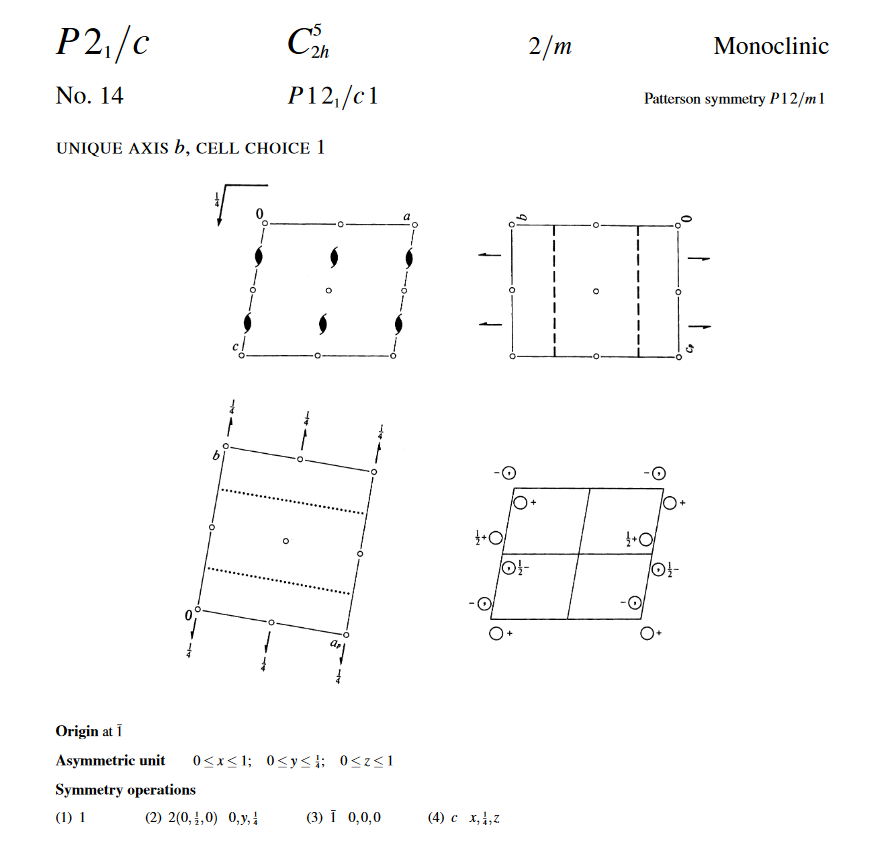
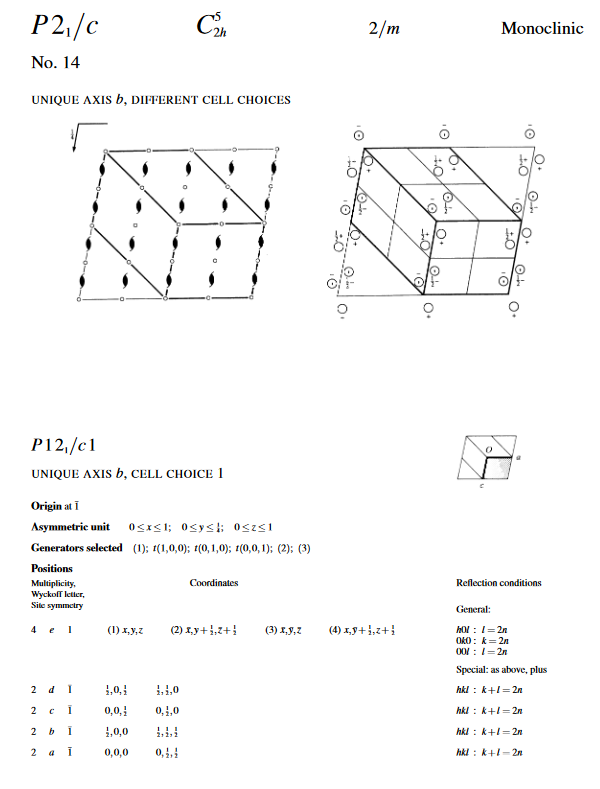
International Tables for Crystallography

Example of Space Group Representation

Examples of polymorphic crystals

Orthorhombic form of S₈

Monoclinic form of S₈

Link ai 230 gruppi spaziali