Symmetry in other spaces

Symmetry Groups in One- and Two-Dimensional Spaces

For structural studies of reactivity and molecular organization on crystalline surfaces (for example, surface studies using techniques such as LEED (Low Energy Electron Diffraction) and ESCA (Electron Spectroscopy for Chemical Analysis) for analyzing gas adsorption on metal surfaces of interest in heterogeneous catalysis, and for studies of liquid crystals, which exhibit a lower degree of order compared to the 3D order present in crystals (nematic phase with a single preferential orientation, or smectic phase with a layered 2D organization), it is useful also to consider symmetry in spaces with dimensions lower than three.

One-Dimensional Space and Line Groups

In one-dimensional space, the simplest regular arrangement consists of a line of points regularly translated with a periodic repetition corresponding to the one-dimensional lattice with a lattice constant a.

In one-dimensional space, there is only one type of Bravais lattice, the primitive one, with no constraints on the cell parameter and only one symmetry in addition to the trivial one: centrosymmetry.

In one-dimensional space, the symmetry elements, point, axis, and plane orthogonal to the direction of the one-dimensional lattice, collapse into a single symmetry element, denoted as m in the International Tables for Crystallography. Moreover, there are no additional symmetry elements involving translation other than the lattice translation itself. Therefore, in one-dimensional space, there are only two line groups: p1 and pm.

Two-Dimensional Space and Plane Groups

Moving on to regularly arranged points in a plane, five possible two-dimensional lattices belong to four crystal systems (with two lattices within the rectangular system).

Oblique lattice with no constraints on the cell parameters.

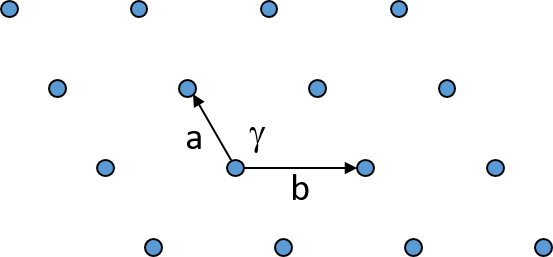
Primitive rectangular lattice with the constraint of angle γ = 90°.

Centered rectangular lattice with the constraint of angle γ = 90°.

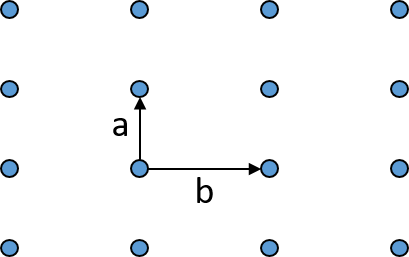
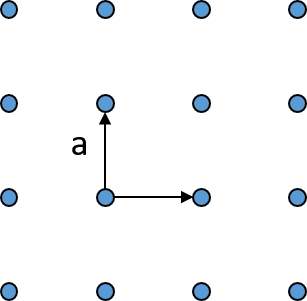
Square lattice with the constraints a = b and angle γ = 90°.

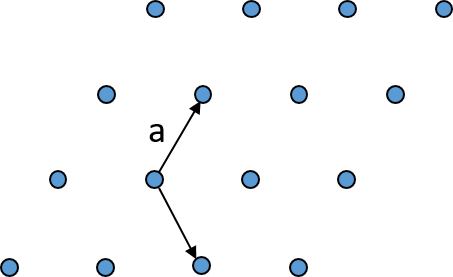
Hexagonal lattice with the constraints a = b and angle γ = 120°.

In two-dimensional space, the symmetry elements of an inversion center and a twofold rotation axis perpendicular to the plane are equivalent (by convention, this symmetry is represented by the perpendicular twofold axis, 2). Similarly, a reflection plane perpendicular to the 2D space coincides with a twofold rotation axis obtained by the intersection between the mirror plane and the 2D lattice plane (by convention, this symmetry is represented by the perpendicular mirror plane, m).

The only symmetry elements involving translation that are compatible with a two-dimensional lattice are glide planes (g).

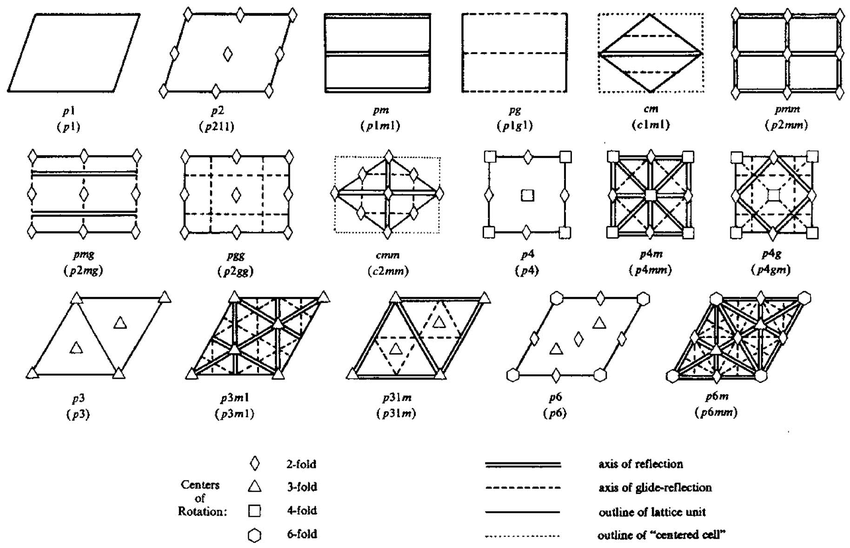
There are a total of 17 plane groups (also known as wallpaper groups):

• 2 in the oblique system (p1 and p2)

• 7 in the rectangular system (5 primitive: pg, pm, pgg, pmg, and pmm; and 2 centered: cm and cmm)

• 3 in the square system (p4, p4g, and p4m)

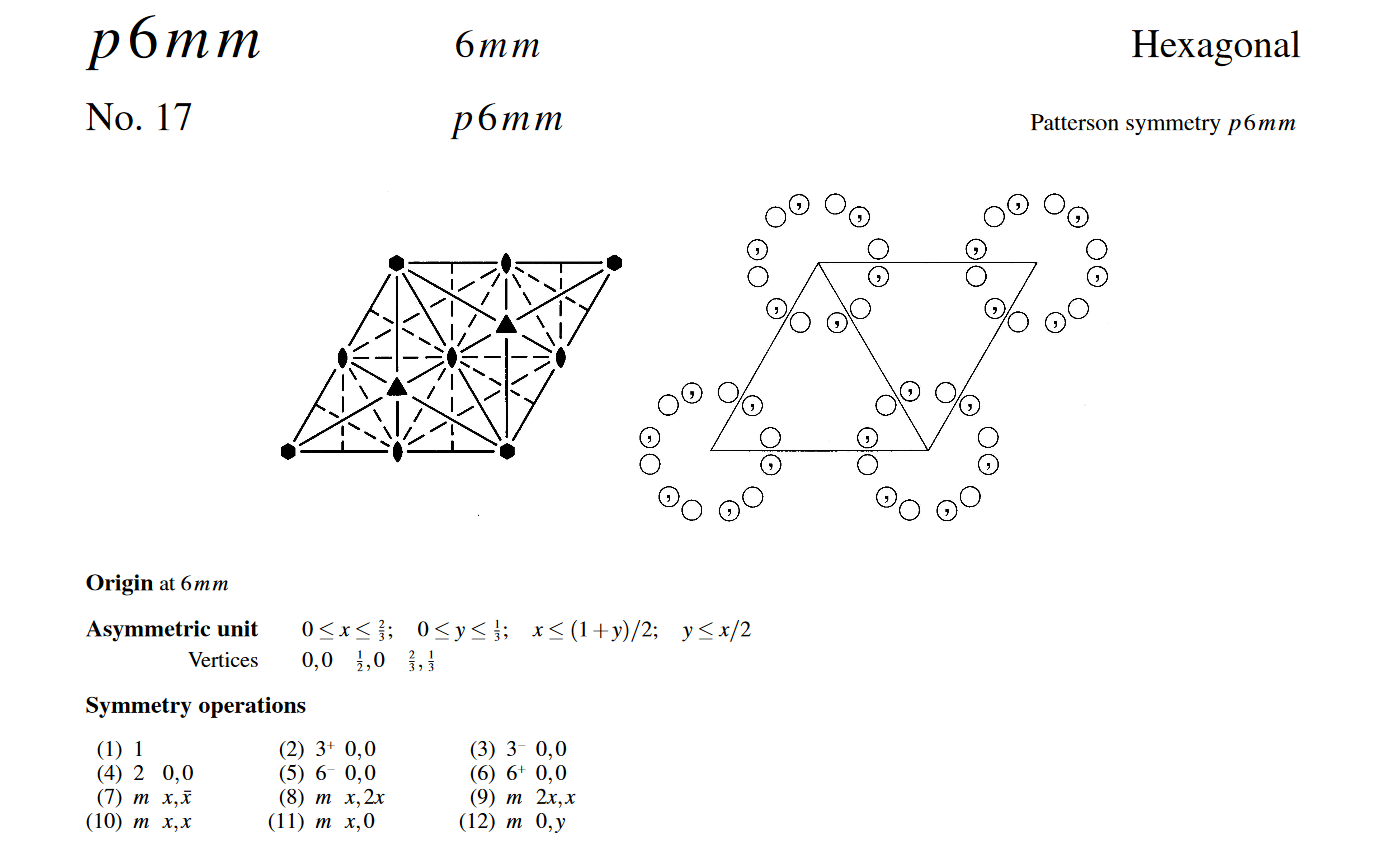
• 5 in the hexagonal system (p3, p31m, p3m1, p6, and p6m)

International Tables for Crystallography

Example of representation of a plane group.

Escher's paintings

Find the wallpaper group of the following paintings by Escher.

Space with More Dimensions and Color Symmetry Groups

Three-dimensional Euclidean space may not be sufficient to describe the symmetries of objects with certain properties. Therefore, one or more continuous variables (e.g., time, the phase of a wave function, etc.) can be added, formally expanding from a 3-dimensional space to an n-dimensional space with n >3. Naturally, the complexity in handling this symmetry increases significantly; for example, there are 4894 space groups in 4 dimensions compared to 320 in 3D space.

The additional variables in three-dimensional space can also be discontinuous and dichotomic, taking only two possible values (e.g., spin). Groups where three variables correspond to 3D Euclidean space, while the fourth has a different physical meaning and is discontinuous in a dichotomic manner, are of considerable importance in Crystallography.

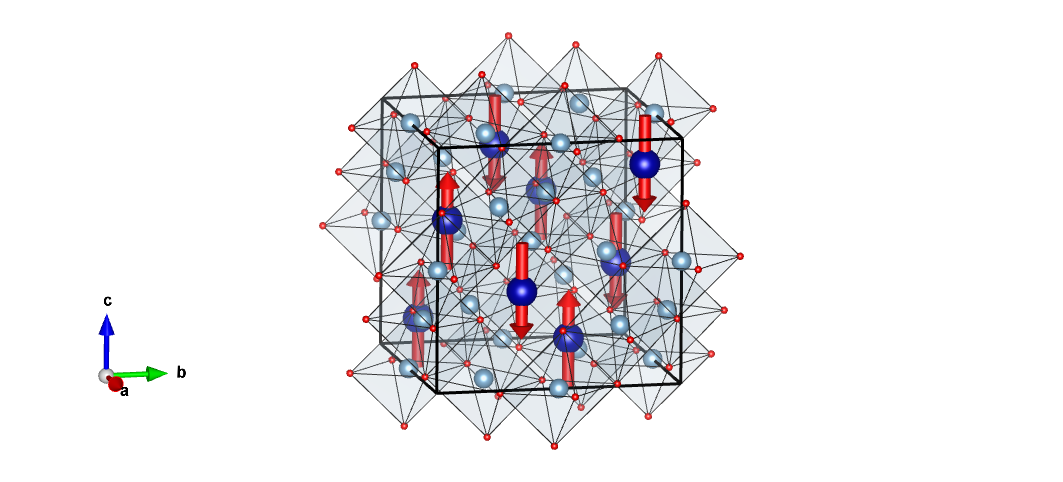
For example, the position and orientation of the magnetic moments of cobalt atoms in the CoAl₂O₄ structure (whose space group is Fd$\bar{3}$m) can be described in the magnetic space group I4₁'/a'm'd, where, in addition to the symmetry operations already encountered, the antisymmetric operation 1' is present. This operation changes the orientation of the magnetic vector, without altering the position of the atoms. Groups that contain this element are also called groups with antisymmetry. Thus, while spatial symmetry operators change the coordinates, the antisymmetry operator inverts the magnetization direction, or, more generally, in a structure with a bicolored property (black and white), it swaps the two colors. Symmetry operators that change the color are denoted with an apostrophe; for example, 4₁ becomes 4₁' and m becomes m'. 4₁' is the symmetry element that successively rotates the object by 90°, translates it by 1/4 of the unit cell along the axis, and changes its color, while the symmetry element m' reflects the object and changes its color.

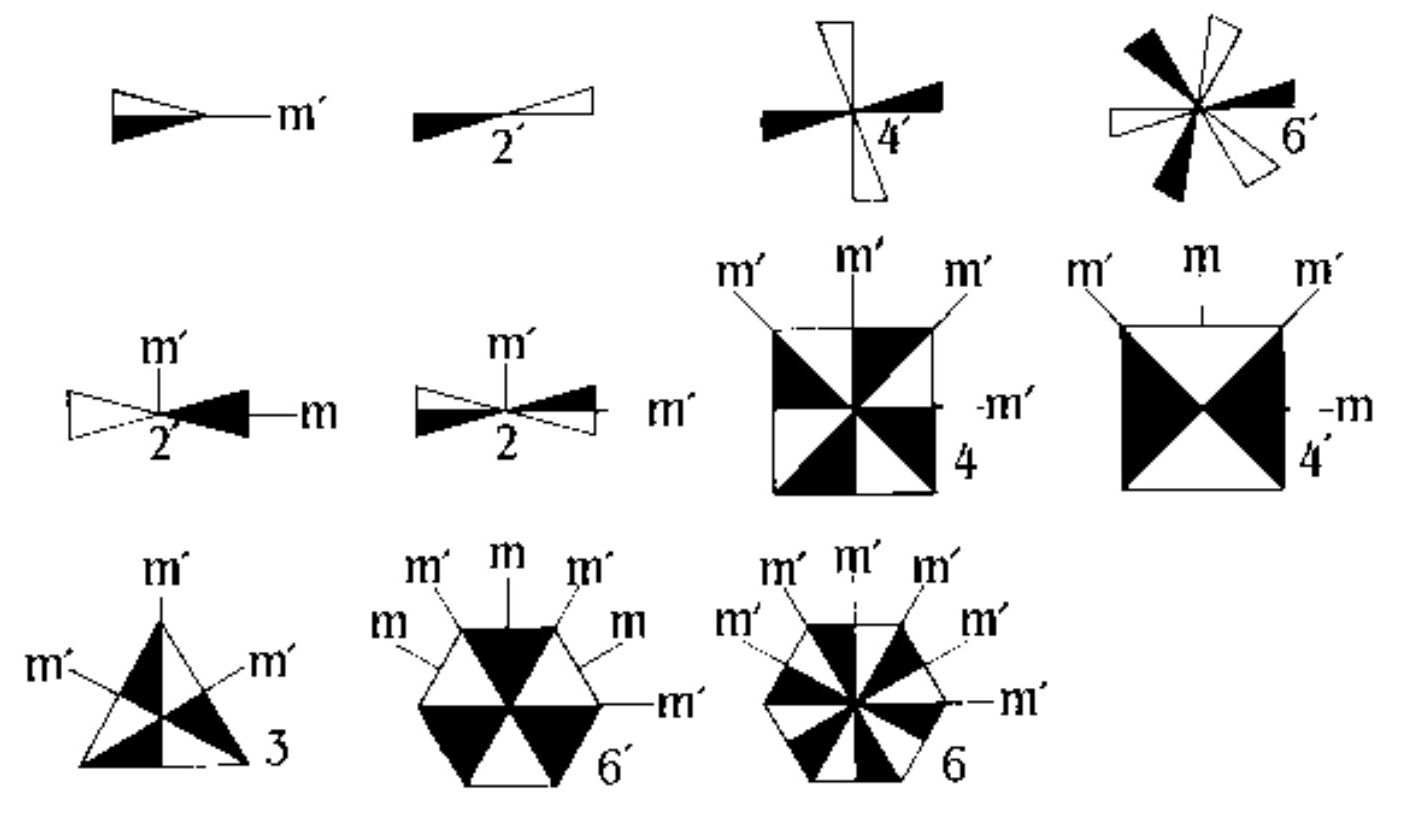
Diagram of Additional Point Color Symmetry Operations.

The 230 space groups generate a total of 1651 types of magnetic space groups.