Other Types of Unconventional Unit Cells
Unconventional Unit Cells
The unit cells underlying the 14 Bravais lattices have the characteristics conventionally required for a unit cell: the smallest possible volume, consistent with the symmetry of the crystal system.
However, it has been shown that primitive unit cells P can be identified for all centered cells C, F, or I. Unlike the conventional non-primitive unit cells, these primitive cells do not adhere to the symmetry constraints of the system in question.
For example, the primitive cell for a cubic F lattice is a rhombohedral cell with all equal axes and all angles equal to 60°, while the primitive cell for a cubic I lattice is a rhombohedral cell with α = 109°28'.
Naturally, these primitive cells, though unconventional, correctly generate the entire lattice and are sometimes used because they have the advantage (especially from the perspective of solid-state physicists) of containing only one lattice node, compared to the 2 nodes in C and I cells and the 4 nodes in F cells.
Wigner-Seitz Cells
In general, the conventional unit cell is a parallelepiped and, as such, can be considered a particular polyhedron.
Many families of polyhedra can fill space by translation.
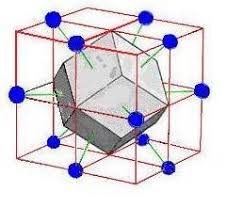
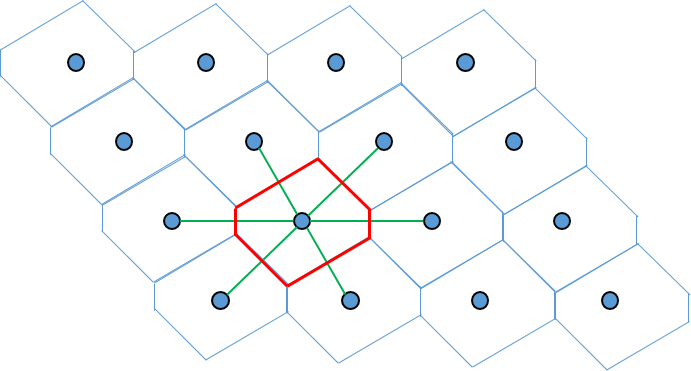
One important type of polyhedron is obtained through the Dirichlet construction: Each lattice point is connected by line segments to its nearest neighbors; At the midpoints of these segments, planes perpendicular to the segments are constructed; The intersection of these planes defines a region of space known as the Dirichlet region, or more commonly, the Wigner-Seitz cell.
Example of a Wigner-Seitz cell in two-dimensional space.
Esempio tridimensionale di cella Wigner-Seitz