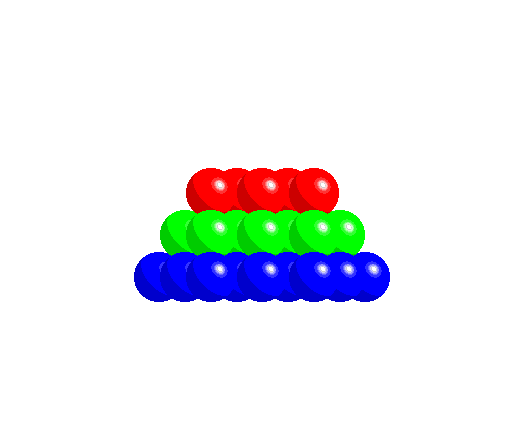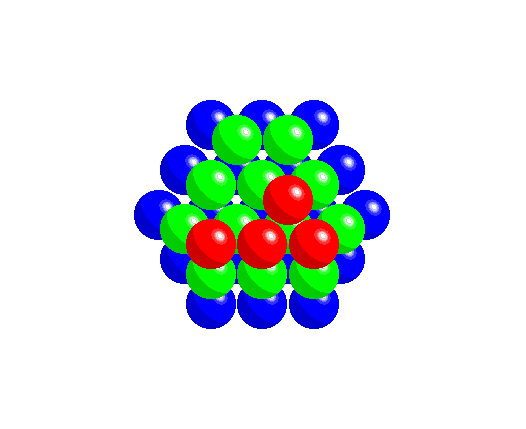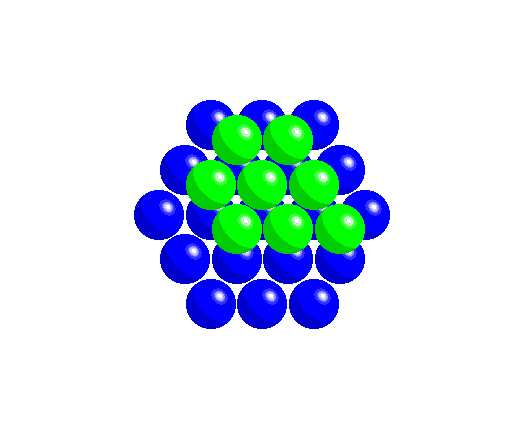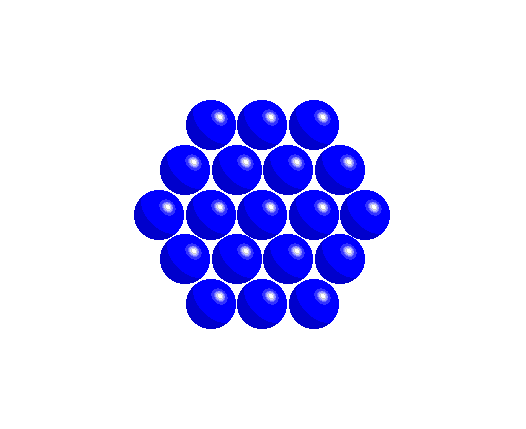Sphere packing
Sphere Packing
The roughly spherical shape of isolated atoms and atomic ions makes studying the packing of rigid spheres quite natural. This approach is particularly useful for understanding the structure of metallic and ionic systems, which are characterized by isotropic, spherically symmetric interactions. These systems typically exhibit high coordination numbers, and in some cases, it can even be difficult to define the coordination number unambiguously due to the presence of multiple interaction levels between atoms, with only small differences in coordination distances.
Two-Dimensional Packings
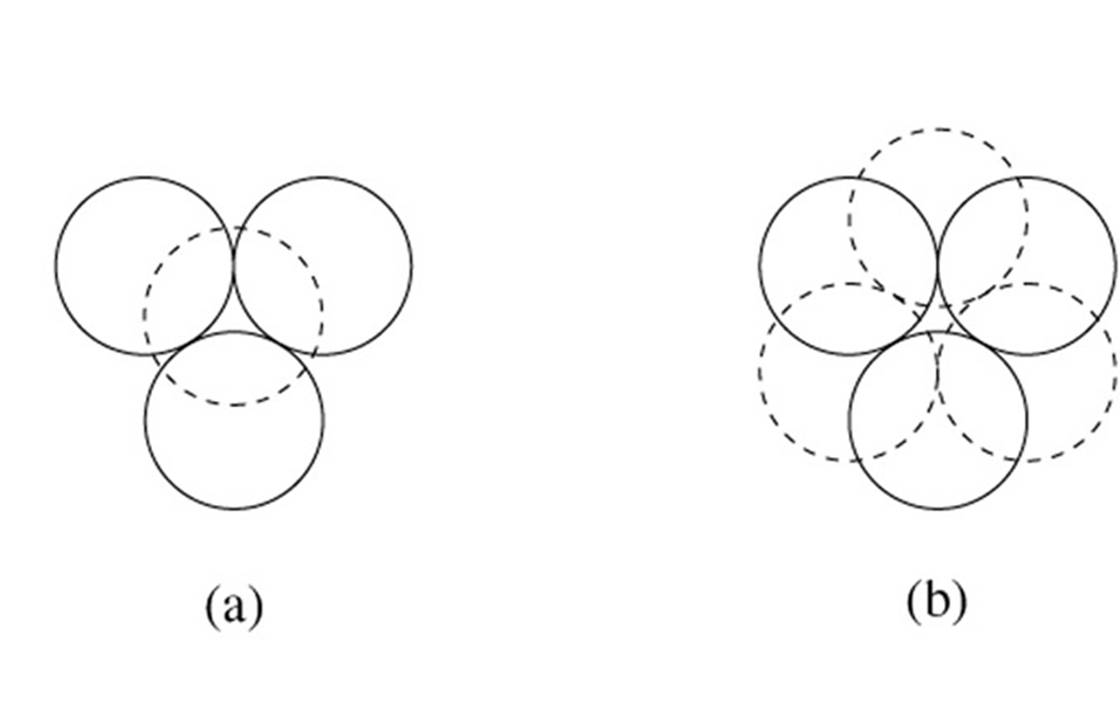
There are two regular ways to arrange rigid spheres in contact within a plane, and both correspond to two-dimensional lattice symmetries.
In the first case, the spheres are arranged at the nodes of a square lattice (point symmetry 4mm), with each sphere in contact with four others (coordination number, c.n. = 4).
In the second case, the spheres are arranged at the nodes of a hexagonal lattice (point symmetry 6mm), where each sphere is in contact with six others (c.n. = 6).
This second arrangement can also be viewed as derived from the first square structure by sliding entire rows of spheres so that they fit into the gaps between spheres of adjacent rows. This second method of arranging the spheres results in the most efficient packing (i.e., it leaves the least empty space) and forms a compact layer (close-packed, cp packing).
In fact, considering the plane where the spheres touch, the circles of radius r occupy an area of πr² each. The square lattice is primitive, meaning that a cell of area 4r² contains one full circle. The percentage of the area occupied by the circles relative to the total plane area is thus (π/4) × 100 = 78.5%.
In the second case, the hexagonal lattice, being also primitive, contains one full circle per unit cell, but the cell area is smaller than in the square lattice because of the angle γ = 120°.
The cell area is given by 4r²sin(120°) = 4r²√3/2.
Thus, the percentage of space occupied by the circles in this arrangement is higher, namely (π/2√3) × 100 = 90.7%.
Given N spheres, the first (square) packing generates N sites surrounded by 4 spheres, while the compact (hexagonal) packing generates 2N sites, each surrounded by 3 spheres.
The maximum radius of a sphere that can be hosted at the center of these sites is related to the radius of the spheres forming the lattice in the plane.
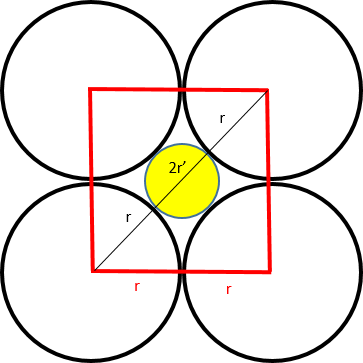
In the case of square packing, the cell with side length 2r can host a sphere at the center of the lattice.
The diagonal of the cell equals the sum of the diameters of the two spheres if the internal sphere fully occupies the available space (2r + 2r').
Given that the diagonal d = √2 × 2r = 2r + 2r', it follows that r' = r(√2 - 1), and thus the ratio r'/r = 0.414.
Therefore, in square packing, a sphere with a maximum radius equal to 0.414 times the radius of the main spheres can be hosted with square coordination.
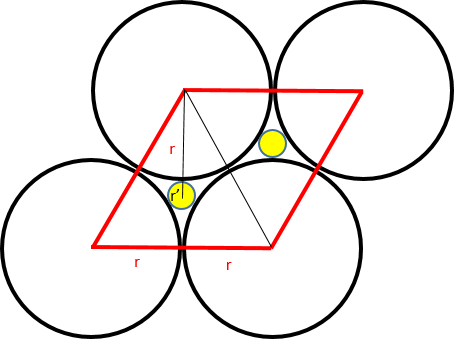
In the case of close packing, the hexagonal cell with side length 2r can host two smaller spheres with trigonal coordination, each placed at the center of an equilateral triangle with side length 2r.
Considering that the height of the triangle is √3r, and that the centroid lies at 2/3 of the height from the vertex, and given that the distance from the centroid to a vertex equals the sum of the radii of the two spheres, we have:
r + r' = (√3r) × (2/3),
from which it follows that:
r' = r(2/√3 - 1),
thus giving the ratio r'/r = 0.155.
Therefore, in hexagonal packing, a sphere with a maximum radius equal to 0.155 times the radius of the main spheres can be hosted with trigonal coordination.
This sphere is therefore much smaller than the one that can fit into the square lattice.
Three-Dimensional Packings
In three-dimensional space, various ways exist to arrange spheres to generate a lattice.
If the coordination number is low, for example, 4 as in the case of diamond, the packing density (the fraction of total space occupied by the spheres) is very low.
For instance, if we consider a hypothetical structure where the spheres are in contact at the midpoint of the bonds of a diamond lattice (covalent radius), the packing density is only 0.340.
Arrangements of this type, with low coordination numbers and therefore low packing efficiency, are stable only in the presence of covalent bonds linking the spheres together.
These types of structures are thus better described as networks of covalent bonds rather than as sphere packings.
Therefore, here we will focus only on packings where the spheres are in contact with six or more neighbors.
Simple Cubic Packing (c.n. = 6)
By stacking square layers of spheres, a primitive (simple) cubic packing can be obtained.
This type of packing results in a coordination number of 6 for each sphere.
Specifically, each sphere is in contact with six other spheres located at the vertices of an octahedron, with the contacts occurring along the edges of the primitive cubic cell, which has a cell edge of a = 2r.
The space group of this packing is Pm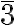 m.
m.
There are no sphere contacts along the face or body diagonals. Just over half of the space is occupied by the spheres.
The low coordination number and the low density (π/6 ≈ 0.524) make this structure unsuitable for metals; the only known case is that of α-Polonium (α-Po).
Mercury, however, crystallizes with a structure similar to that of polonium, in which the atoms maintain a coordination number of 6.
This structure can be derived from the primitive cubic packing by stretching along one of the four cube diagonals, so that the cube becomes a rhombohedron (with cell angles of 70.5° instead of 90°).
Simple Hexagonal Packing (c.n. = 8)
By stacking aligned hexagonal layers of spheres, a primitive hexagonal packing (P6/mmm) can be obtained, with cell parameters a = c = 2r (simple).
This type of packing results in a coordination number of 8 for each sphere (6 contacts within the hexagonal plane, plus one above and one below the plane).
Although the density is higher than that of simple cubic packing (π/6 × 2/√3 ≈ 0.605), the contrast between the compact packing within the hexagonal layer and the much less compact stacking of layers along the c-axis makes this type of structure unlikely.
For example, no metals are known to adopt this type of structure.
However, even though no metals crystallize with a simple hexagonal packing, there are some known interstitial derivatives.
For instance, in AlB₂, boron atoms occupy trigonal prismatic cavities within the simple hexagonal packing of aluminum.
or WC, where the simple hexagonal packing of tungsten is present, with half of the trigonal prismatic cavities occupied by carbon.
Body-Centered Cubic Packing (c.n. = 8)
An arrangement with the same coordination number of 8 as simple hexagonal packing, but much more significant, is body-centered cubic (bcc) packing.
This type of packing, although it does not feature compact hexagonal layers, is denser and more balanced in terms of empty spaces. The spheres occupy the vertices and the center of the cubic cell, and are therefore in contact along the diagonals of the cube.
Considering the spheres in contact (with a radius of √3/4 a, where a is the cell edge), and noting that there are two spheres per cell, the density is given by:
2 π √3 / 4² = 0.680.
This type of crystalline packing, with the space group Im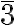 m, is adopted by a large number of metals.
m, is adopted by a large number of metals.
Vanadium Structure
Although each sphere is directly in contact with only 8 other spheres, there are also 6 additional neighbors (second coordination sphere) at a distance just 15% greater (cell edge = 2/√3 the diameter of the sphere).
For the atom located at the center of the cell, these 6 neighbors are at the centers of the 6 adjacent cells. Therefore, for this type of packing, the coordination number could also be considered as 14. In this case, the corresponding coordination polyhedron would be a truncated octahedron rather than a cube.
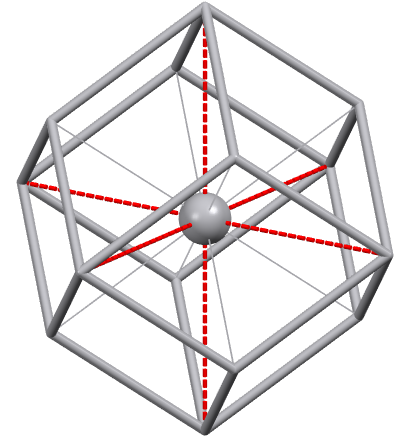
Although bcc packing is less dense than compact packings (as we will see below) and therefore contains more empty space for interstitial ions, interstitial structures based on this arrangement are rare.
An example is the alpha form of silver iodide, where the silver ion is statistically disordered within the distorted tetrahedral sites. This contrasts sharply with the numerous interstitial structures found in compact packings.
bcc packing produces both distorted octahedral and tetrahedral sites. The distortion of the octahedral sites is evident when considering that of the six spheres defining the site, two are at a distance of half the cell edge from the center of the site, while the other four spheres are positioned along the diagonal of the cell, and thus are at a distance √2 times greater.
In a single cell, we can identify one octahedral site on each face and one octahedral site on each edge. Therefore, the total number of octahedral sites formed in a bcc packing of N spheres is 3N, and the maximum radius of the sphere that can fit in these sites is 0.155r.
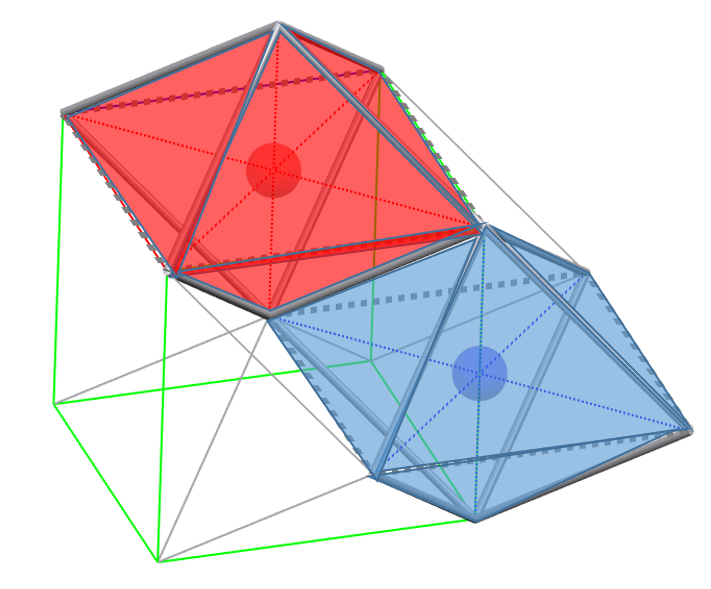
Within the octahedral sites, we can identify 4 equivalent distorted tetrahedral sites, considering that these sites are present both in the octahedra with the center located on the faces and those with the center located on the edges of the cell.
Therefore, the total number of tetrahedral sites formed in a bcc packing of N spheres is 6N, and the maximum radius of the sphere that can fit into these sites is 0.291r.
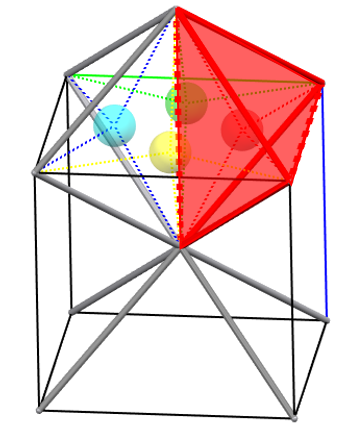
It is interesting to observe that the number of distorted octahedral and distorted tetrahedral sites is higher in both cases than what we encounter in compact packings. Furthermore, the maximum radius of a sphere that can fit into the distorted tetrahedral sites is greater than that which can fit into the distorted octahedral sites (exactly the opposite of what we will see for compact packings).
Tetragonal Body-Centered Packing (c.n. = 10)
In bcc, the small difference of 15% between the first coordination distances (8 nearest neighbors) and the second coordination distances (6 second nearest neighbors) suggests the possibility of achieving, through a deformation of the cubic structure, packings with coordination numbers intermediate between 8 and 14.
Considering that the 6-second nearest neighbors are arranged according to an octahedral geometry, one could deform the structure by compressing or elongating the cell in a given direction (tetragonal deformation).
By applying tetragonal compression (c < a), we bring the two axial atoms closer to the first nearest neighbor atoms, while the other 4 distances (the equatorial atoms) remain unchanged.
By elongating the cell (c > a), we move the two axial atoms farther apart, as well as the first nearest neighbor atoms relative to the equatorial atoms.
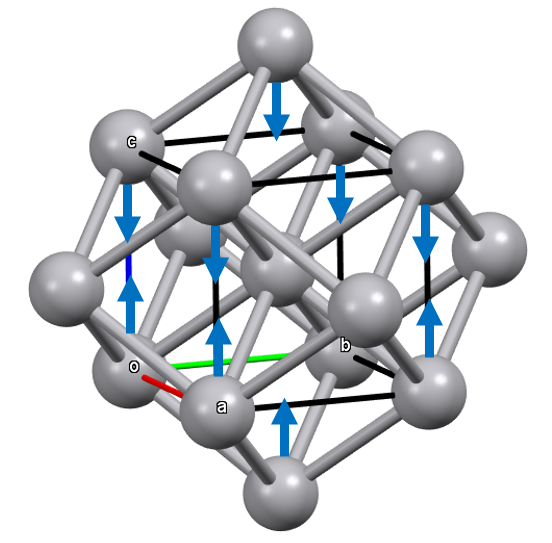
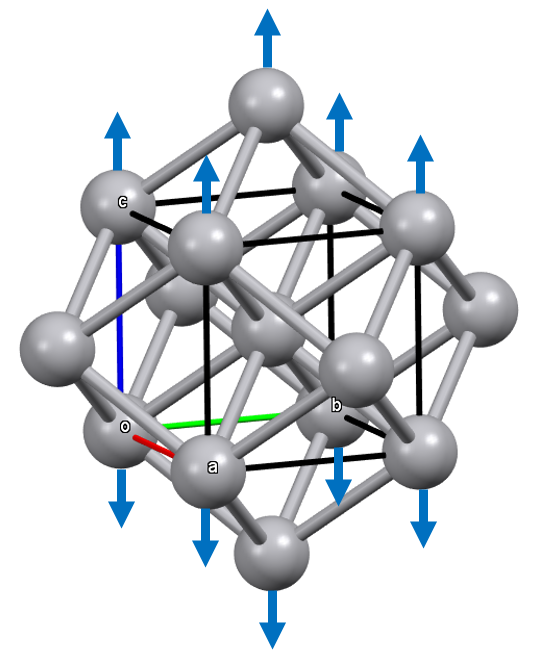
Therefore, it is possible through these tetragonal deformations to achieve new limit packings in which the coordination number increases from 8 to 10 through compression, or from 8 to 12 through elongation.
In the first limit case of tetragonal deformation by compression, an ideal bct structure with c.n. 10 is obtained when c² = 1/2 a² + 1/4 c², which simplifies to c = a √(2/3).
This structure, with a density of 0.698, slightly higher than that of bcc, can be seen as derived from compact hexagonal planes stacked in such a way that individual spheres are placed between pairs of spheres from the adjacent layer. This is a more efficient way of packing spheres compared to simple hexagonal packing, but as we will see, it is less efficient than close-packed structures, where the spheres fit into trigonal sites.
Only one metal, protactinium (Pa), crystallizes with the tetragonal body-centered structure, having a nearly ideal coordination number of 10.
In the second case of tetragonal deformation by elongation, a limit structure with c.n. 12 is achieved when a² = 1/2 a² + 1/4 c², which simplifies to c = a √2, corresponding to a compact fcc packing.
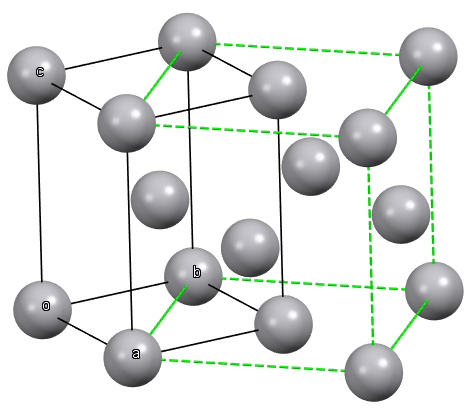
Compact Packings (c.n. 12)
To achieve a three-dimensional compact packing, the two-dimensional compact layers must be arranged in such a way that they partially fill the trigonal interstices present in the layers. Each sphere thus comes into contact with three spheres from the layer below, three spheres from the layer above, in addition to the six spheres from the same layer.
This generates two different types of three-dimensional interstices: 2N smaller tetrahedral interstices bounded by 4 ions (three from the same layer and one from the adjacent layer), and N larger octahedral interstices bounded by 6 ions (three from the same layer and three from the adjacent layer).
The compact packing has a density of π/(3√2) = 0.740, and the volume of the empty space in an octahedral site bounded by 6 spheres is greater than the empty space bounded by the four spheres of the tetrahedral site. The maximum radius of a sphere that can be accommodated in these sites is 0.225r for the tetrahedral sites and 0.414r for the octahedral sites. The 2N tetrahedral sites can be distinguished into N positive tetrahedral sites and N negative tetrahedral sites depending on their orientation relative to the layers.
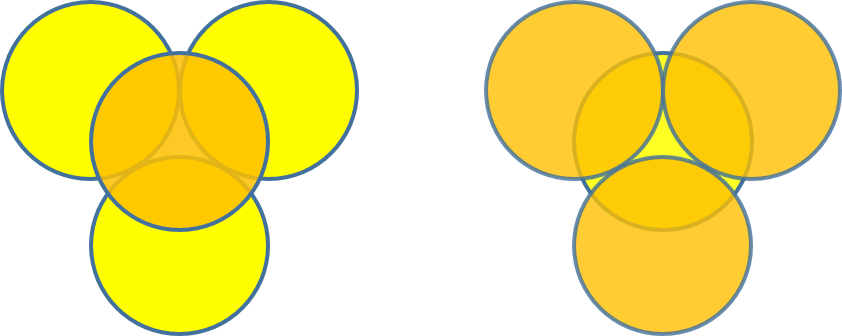
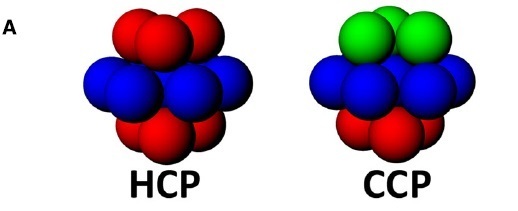
The compact packing has two main possible variations that differ in the relative arrangement of the layers: hexagonal close packing and cubic close packing.
In hexagonal close packing, the layers above and below a given layer are arranged exactly over each other (eclipsed) when the structure is observed orthogonally to the layers. As a result, the octahedra in the subsequent layers share faces and form columns of adjacent octahedra, just as the tetrahedral sites align in columns alternating between positive and negative sites.
While in cubic close packing, the layers above and below a central layer are staggered, and the spheres of one layer align with the octahedral sites defined by the upper layer, and vice versa.
The corresponding polyhedra with c.n. 12 are, for cubic close packing: the cuboctahedron (an Archimedean solid with point symmetry Oh m m), and for hexagonal close packing: the triangular orthobicupola (a Johnson solid with point symmetry D3h
m), and for hexagonal close packing: the triangular orthobicupola (a Johnson solid with point symmetry D3h  m2), both characterized by 6 square faces and 8 triangular faces. However, while both solids are made up of regular polyhedra, the Archimedean solids have all vertices equivalent, whereas the Johnson solids do not.
m2), both characterized by 6 square faces and 8 triangular faces. However, while both solids are made up of regular polyhedra, the Archimedean solids have all vertices equivalent, whereas the Johnson solids do not.
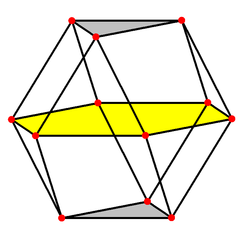
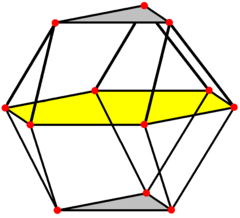
The cubic close packing translates into a face-centered cubic structure Fm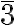 m with a lattice constant a = √23r = 2.828r, with the atom at the origin in the special Wickoff position with multiplicity 4 and symmetry m
m with a lattice constant a = √23r = 2.828r, with the atom at the origin in the special Wickoff position with multiplicity 4 and symmetry m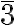 m. The compact layers are arranged perpendicular to the diagonals of the face-centered cubic cell.
m. The compact layers are arranged perpendicular to the diagonals of the face-centered cubic cell.
The hexagonal close packing translates into a hexagonal cell with a = 2r and c = √25/√3r = 3.266r (c/a = 1.633) and symmetry P63/mmc, with the atom in the special Wickoff position (1/3, 2/3, 1/4) with multiplicity 2 and symmetry 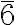 m2. The compact layers are arranged perpendicular to the c direction of the hexagonal cell.
m2. The compact layers are arranged perpendicular to the c direction of the hexagonal cell.
Layer Sequence
Given a compact layer with orientation A, we have seen that the next layer can result in a compact packing if its orientation is of type B or C (c.n. 12). An hexagonal close packing is obtained if the layers with orientations A and B are alternately arranged (ABABAB...), or cubic close packing if the layers with orientations A, B, and C are arranged in this repeated sequence (ABCABCABC...). Meanwhile, if the stacking is done with an alternating arrangement of layers A and D (ADADAD...), with spheres placed between pairs of spheres in layer A, a tetragonal body-centered packing (bct) (c.n. 10) is obtained. If the subsequent layers always have the same orientation A (AAA...), the result is a simple hexagonal packing (c.n. 8).
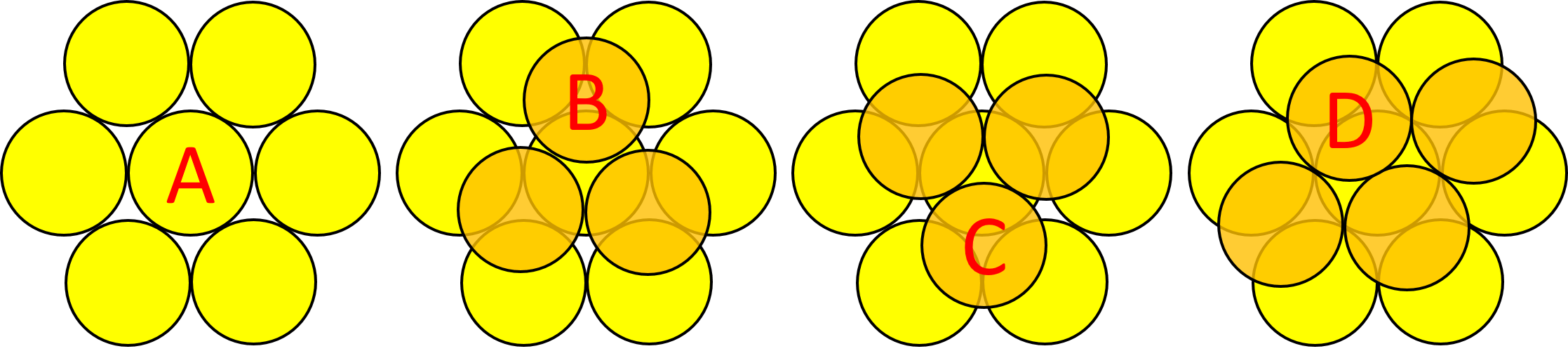
We have seen that metals do not crystallize in simple hexagonal packing (c.n. 8); in fact, just a small relative shift of the atoms is enough to achieve a structure with a higher coordination. However, coordination 8 is found in the body-centered cubic (bcc) system with a more efficient packing, which is indeed adopted by a large number of metals (Fe, Cr, Mo, W, Ta, Ba, V, ...).
Structures with c.n. 10, as we have seen, are very rare (Pa), and many metals prefer to arrange themselves in one of the two compact structures. For example, among the metals that adopt hexagonal close packing (hcp) are Be, Mg, Zn, Co, Cd, Ti, Zr, ...
Structure of Co
While among those that adopt cubic close packing (ccp) we find: Cu, Ag, Au, Al, Ni, Pb, ....
Structure of Au.
Like pure metals, many alloys (intermetallic phases or solid solutions) also show compact structures. For example, Cu and Au have ccp structures, both as pure elements and when mixed to form Cu-Au alloys.
Structures with c.n. 6 cubic simple, as we have seen, are instead very rare (Po).
There are, and have been observed in some materials, more complex sequences of compact layers in which the sequence, although regular, is of a mixed type compared to the repeated sequences of compact layers in ccp and hcp packings. For example, regular arrangements can be found in which, between layer B and C of ccp, another layer with orientation A is introduced, forming a sequence of the type ABACABAC..., which generates, therefore, between ccp-type layers also layers with hcp-type packing. These more complex situations are represented by indicating the sequence of layers with the letters h and c if the preceding and following layers are, respectively, the same or different. For example, in the previous case with the repeated sequence of the type ABAC, the packing is of the hc type. This variety of situations is related to a phenomenon called polytypism.
Some metals exhibit cases of these complex sequences.
For example:
hc: La, Pr, Nd, Am
The α form of La has an hc structure, also called double hexagonal close-packed (dhcp) (the β form is ccp, and the γ form is hcp).
chh: Sm.
The α form of Sm has a chh structure with a rhombohedral unit cell (the β form is hcp, and the γ form is bcp, and there is also a dhcp form that is obtained under high pressure and temperature).
In general, the great frequency of more compact structures arises from the fact that in many halides, oxides, and sulfides, the anions are significantly larger than the metal ions and are arranged according to one of the two most compact packings, hcp or ccp. The metal ions (generally smaller) occupy the interstitial sites between the compact anion layers. On the other hand, in a different and larger class of compounds, the opposite occurs. For example, in interstitial borides, carbides, and nitrides, the non-metallic atoms occupy the interstices between the compact layers formed by the metals. Thus, in many ionic solids, the larger ion often assumes a compact type of packing, and depending on the size and stoichiometry of the ions present in the compound, the octahedral and/or tetrahedral sites can be completely or partially occupied by the smaller ions.
However, often the counterions may be too large for the interstitial sites, and thus the structure can only accommodate them by expanding the compact lattice. As a result, the compact arrangement of ions with a larger radius remains the same as the compact packing, but these ions cannot be in direct contact with each other as in the ideal compact structure. The term eutactic (and eutaxy) is used to refer to structures like these in which the packing is loosened due to the interstitial ions.
For subsequent reference structures, the terms ccp and hcp are used extensively, considering lattice structures of ions that are not necessarily in contact, and thus eutactic structures are also included.
It is rare for all interstitial sites in a compact packing structure to be occupied simultaneously. Very often, a set of octahedral or tetrahedral sites is completely or partially populated, while the others remain empty.
ccp packing of N anionic spheres A⁻ with some sites fully occupied
|
N Octahedral sites, O |
ALL Occupied |
EMPTY |
EMPTY |
|
N Tetrahedral sites, T+ |
EMPTY |
ALL Occupied |
ALL Occupied |
| N Tetrahedral sites, T- |
EMPTY |
EMPTY |
ALL Occupied |
|
STRUCTURE |
NaCl |
ZnS sphalerite (zinc blende) |
Na2O antifluorite |
|
COORDINATION |
Na+ 6, octahedral Cl- 6, octahedral |
Zn2+ 4, tetrahedral S2- 4, tetrahedral |
Na+ 4, tetrahedral O2- 8, cubic |
| Other compounds with this structure |
MgO, CaO, TiO, MnO, NiO, CoO, TiC, MgS, CaS, MgSe, BaTe, LiF, LiCl, NaBr, NaI, NaH, TiN, AgCl, AgBr |
CuF, CuCl, SiC (beta) BN, BP, BaS, GaP, GaS, AlP, InAs, C diamond (C in both positions), Si, Ge |
Li2O, Li2S, Na2S, K2S, K2Se, K2Te |
ccp type like sodium chloride (NaCl) with all octahedral sites occupied. Both ions are arranged in a ccp structure.
ccp type like sphalerite (ZnS), where only one type of tetrahedral site is occupied by Zn²⁺ ions.
ccp type like antifluorite (Na₂O) with all tetrahedral sites occupied.
Fluorite (CaF₂) has the same type of packing but with reversed roles, where the positive ions form the ccp structure and the fluoride ions occupy the tetrahedral interstitial sites.
hcp packing of N anionic spheres A⁻ with some sites fully occupied
|
N Octahedral sites, O |
EMPTY |
ALL Occupied |
|
N Tetrahedral sites, T+ |
ALL Occupied |
EMPTY |
| N Tetrahedral sites, T- |
EMPTY |
EMPTY |
|
STRUCTURE |
ZnS (Wurtzite) |
NiAs (Nickel arsenide) |
|
COORDINATION |
Zn2+ 4, tetrahedral S2- 4, tetrahedral |
Ni3+ 6, Octahedral As3- 6, Trigonal prismatic |
|
Other compounds with this structure |
ZnO, BeO, CdS, MnS, AgI, AlN, GaN, InN, SiC |
NiS (As, Sb, Se, Te) FeS, FeSe, CoS (Se,Te) MnAs (Sb, Te) |
hcp type wurtzite ZnS: only one type of tetrahedral site is fully occupied.
hcp type NiAs (Nickel Arsenide): the octahedral sites are fully occupied, and the coordination of the anion is trigonal prismatic.
ccp packing of N anionic spheres A⁻ with some sites partially occupied
|
N Octahedral sites, O |
1/2 Occupied |
1/2 Occupied |
1/3 Occupied |
|
N Tetrahedral sites, T+ |
1/8 Occupied |
EMPTY |
EMPTY |
| N Tetrahedral sites, T- | 1/8 Occupied | EMPTY | EMPTY |
|
STRUCTURE |
MgAl2O4 spinel | CdCl2 | AlCl3 |
| COORDINATION |
Mg2+ 4, tetrahedral Al3+ 6, octahedral |
Cd2+ 6, octahedral | Al3+ 6, octahedral |
|
Other compounds with this structure |
CoAl2O4, CuCr2S4, CuCr2Se4, CuCr2Te4, MgTi2O4, Co2GeO4, Fe2GeO4 |
MnCl2, FeCl2, CoCl2, NiCl2, NiBr2, NiI2, CuCl2. |
CrCl3, YCl3 |
Normal spinel structure MgAl₂O₄
An important characteristic, which influences the properties of these materials, is that the distribution of cations in spinels can vary. Two extreme types of cation distribution can be distingusished.
In normal spinels, such as MgAl₂O₄, the cations occupy the sites according to the formula [A]tet[B₂]octO₄,
meaning the A cations occupy the tetrahedral sites and the B cations occupy the octahedral sites.
In inverse spinels, such as CoFe₂O₄, the cations occupy the sites according to the formula [B]tet[A, B]octO₄,
meaning half of the B ions occupy the tetrahedral sites, while the other half of the B ions, along with all A ions, occupy the octahedral sites.
An important example of an inverse spinel is magnetite Fe₃O₄, where half of the Fe³⁺ cations occupy the tetrahedral sites, while the other half, together with Fe²⁺ ions, occupy the octahedral sites.
Normal and inverse spinels represent two extremes of cation distribution.
There are many examples of intermediate structures (partially inverse), such as NiAl₂O₄, MgFe₂O₄, etc.
The structure of cadmium chloride CdCl₂ is common to various types of halides of divalent ions, where the cation occupies half of the octahedral sites in alternating layers.
The structure of aluminum chloride AlCl₃ is common to various types of halides of trivalent ions, where the cation occupies one-third of the octahedral sites.
hcp packing of N anionic spheres A⁻ with some sites partially occupied
| N Octahedral sites, O | 1/2 Occupied | 1/2 Occupied | 1/3 Occupied | 2/3 Occupied |
| N Tetrahedral sites, T+ | 1/8 Occupied | EMPTY | EMPTY | EMPTY |
| N Tetrahedral sites, T- | 1/8 Occupied | EMPTY | EMPTY | EMPTY |
| STRUCTURE | Mg2SiO4 olivine | CdI2 | ZrCl3 | Al2O3 corundum |
| COORDINATION |
Si4+ 4, tetrahedral Mg2+ 6, octahedral |
Cd2+ 6, octahedral | Zr3+ 6, octahedral | Al3+ 6, octahedral |
|
Other compounds with this structure |
CaMgSiO4, CaMnSiO4, Fe2SiO4, Mn2SiO4, CaMgSiO4, CaFeSiO4, CaMnSiO4, LiMnPO4 |
MnI2, FeBr2, FeI2, CoBr2, CoI2 |
BiI3,TiCl3, TiBr3, CrBr3, FeCl3, FeBr3 |
Ti2O3,Cr2O3, Mn2O3, Fe2O3 |
Magnesium, iron, and manganese nesilicates, which constitute the class of olivine minerals, such as Mg₂SiO₄, have in common an hcp packing of oxygen atoms, with silicon atoms placed in tetrahedral sites and magnesium ions in octahedral sites.
Cadmium iodide (CdI₂) has an hcp packing of iodide ions, with half of the octahedral sites occupied by cadmium ions in alternating layers. Several halides of divalent transition metals have an isomorphic structure to CdI₂.
The tetragonal structure of rutile, a mineral form of titanium dioxide (TiO₂), also exhibits an hcp anionic lattice, but in a distorted form with half of the octahedral sites occupied. Rutile and fluorite represent the main structural types of the AX₂ stoichiometry. For example, the main mineral of tin, cassiterite (SnO₂), has the rutile structure, as well as several fluorides (MgF₂, NiF₂, ZnF₂, CrF₂, MnF₂, FeF₂, CoF₂, NiF₂) and other compounds (CrCl₂, V₂O₄).
The structure of zirconium chloride (ZrCl₃) has an hcp packing of chloride ions with one-third of the octahedral sites occupied by zirconium ions. Several halides of trivalent transition metals have an isomorphic structure to ZrCl₃.
Corundum (Al₂O₃) has two-thirds of the octahedral sites occupied by Al³⁺ ions. This type of structure is found in oxides with a +3 oxidation state for elements from Ti to Fe.
Another important structure that can be related to a compact packing is perovskite, with a general formula ABO₃. Calcium titanate (CaTiO₃) can be described as consisting of a ccp packing with the composition ‘CaO₃’, with one-fourth of the octahedral cavities occupied by Ti cations (the octahedral cavities with 6 oxide vertices).
Many crystals with the perovskite structure exist: KNbO₃, KTaO₃, NaNbO₃, NaWO₃, LaCoO₃, LaCrO₃, LaFeO₃, LaGaO₃, LaVO₃, SrTiO₃, SrZrO₃, SrHfO₃, SrSnO₃, SrThO₃, CsCaF₃, KMgF₃, KZnF₃, CsCdBr₃, CsCdCl₃, CsHgBr₃, CsHgCl₃, etc.
Many materials related to the perovskite structure exhibit interesting electrical properties, such as piezoelectricity and high-temperature superconductivity.
In general, in ionic structures, cations occupy sites that are more suitable for their size. Sometimes, they may occupy sites that, from a theoretical point of view, are too small, causing the anions to be pushed apart and expanding the compact structure (as in eutactic structures). Conversely, cations do not tend to occupy sites that are too large for their size, unless the structure itself can be modified, distorting the arrangement of anions to reduce the size of cation sites. This happens in many distorted perovskite structures, where some cations may be too small to occupy the large cavities with 12-fold coordination (cuboctahedral), resulting in strong structural distortion, such as in GdFeO₃. An interesting intermediate situation occurs in certain structures where the cationic sites are only slightly larger than expected, and the cations undergo small displacements, which leads to a high polarizability of the material and the phenomenon of ferroelectricity, as in the case of BaTiO₃. High-temperature superconductors YBCO have a perovskite structure of the type (Y₁/₃Ba₂/₃)CuO₃₋ₓ.
Distorted perovskite structure of GdFeO₃. The FeO₆ octahedra are rotated to form zigzag chains. This reduces the size of the site occupied by gadolinium, with a decrease in the coordination number from 12 to 8.
Perovskite structure of BaTiO₃ with ferroelectric properties.
High-temperature superconducting perovskite structure of the type (Y₁/₃Ba₂/₃)CuO₃₋ₓ.