Coordination polyhedra

Organization of coordination polyhedra

The 'sphere packing' approach is particularly suitable for studying systems with high coordination numbers, such as metals. When the coordination numbers are intermediate (neither too high nor too low), as in many ionic systems, the 'organization of polyhedra' approach can be very useful for rationalizing the crystal structure.

This approach focuses on the coordination numbers of the cations.
The crystal structures are imagined as being built from polyhedra, each centered on a cation, with vertices defined by their nearest anionic neighbors.
The polyhedra are typically connected through shared vertices, edges, or faces.
This perspective is quite natural, especially considering that the crystal shape is generally a convex polyhedron.

We have already seen how internal and external symmetry of crystals are closely related, and how crystal shapes, which can be described by certain polyhedra, are subject to the symmetry constraints imposed by the crystal lattice.
Similarly, the organization of the coordination polyhedra is governed by the same constraints.

In this approach, nearest neighbors (usually anions) of an atom (typically a cation) define a polyhedral coordination group.
The number of vertices of this polyhedron determines the coordination number (c.n.) of the central atom.

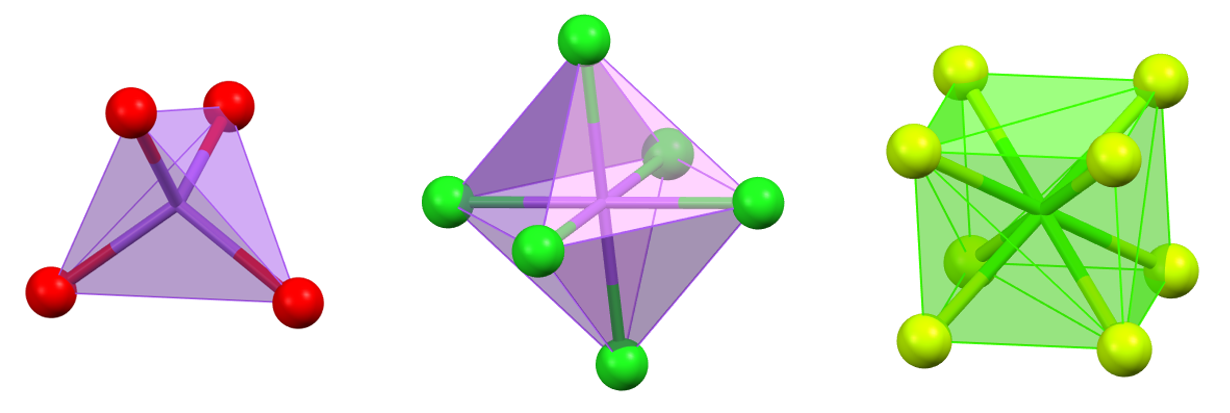
Coordination polyhedra with triangular faces, which represent the most compact arrangements, are the most common.
The most important and frequent coordination polyhedra are the tetrahedron and the octahedron, as their vertices represent the most symmetrical arrangements of 4 or 6 points around a central point.

In terms of coordination polyhedra, a crystal becomes an ordered aggregate of polyhedra joined together through vertices, edges, or faces.

Since the centers of these polyhedra are usually occupied by positive ions, the anionic screening effect and the relative distance between like-charged ions, located at the centers of interconnected polyhedra, generally decrease when moving from a connection through a vertex, to an edge, and finally to a face.

Consequently, it is more common to find polyhedra connected through a vertex rather than an edge, and rarely through a face.

Pauling formalized the rule stating that the sharing of edges, and especially faces, reduces the stability of a structure, particularly for cations with high valence and low coordination numbers, such as tetrahedra containing highly charged cations.

Indeed, when polyhedra share an edge and especially a face, the cation-cation distance decreases, leading to strong electrostatic repulsion between the cations, which becomes even stronger as the ionic charge increases.

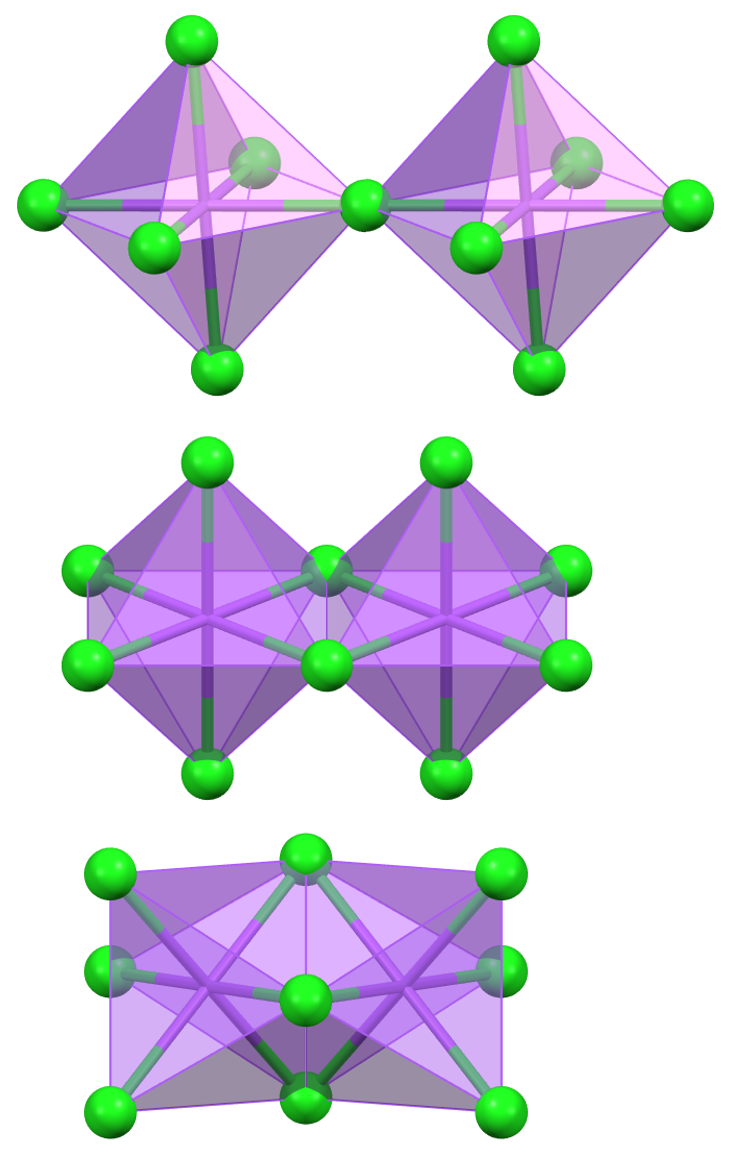
The figure shows how, moving from octahedra sharing a vertex to octahedra sharing an edge, and finally to octahedra sharing a face, the cation-cation distance decreases.

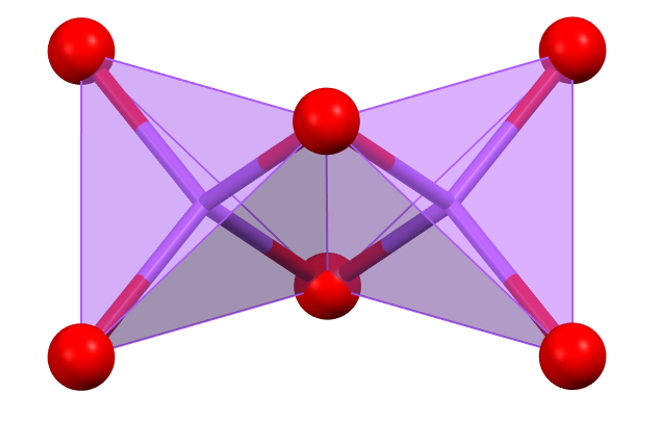
Comparing the situation of octahedra sharing an edge with that of tetrahedra sharing an edge, the cation-cation (M–M) distance (assuming the same cation-anion (M–X) distance) is shorter between the tetrahedra because the MXM angle is 71°, compared to 90° for the octahedra. A similar effect is observed for tetrahedra and octahedra sharing a face.

M–M distances between MX₄ or MX₆ groups sharing vertices, edges, and faces (in terms of M–X).

A strong demonstration of the improbability of having structures with tetrahedra sharing faces (which would bring positive ions closer to each other, compared to negative counterions) is the absolute absence of hcp structures with all tetrahedral sites occupied, and thus constituting the hcp equivalent of fluorite (or antifluorite) ccp. In fact, in sodium oxide (Na₂O) with an antifluorite structure, oxide ions are arranged in a ccp arrangement, and the NaO₄ tetrahedra are connected along the edges. In a structure with an hcp arrangement of anions and all tetrahedral cavities occupied, the tetrahedra MX₄ would instead share faces. While the situation of tetrahedra sharing edges is energetically acceptable, the situation of tetrahedra sharing faces is not.

For tetrahedra containing high-charge cations, the situation of union through edges is not energetically acceptable either, and this can only occur through the vertices of the polyhedron.

For example, in the structures of silicates, consisting of SiO₄ tetrahedra, edges are never shared. In fact, in an ideal ionic structure, the charge on Si would be +4 (even though the actual charge on silicon is significantly lower due to the partial covalency of the Si-O bonds).

Topological Architectures of Joined Polyhedra

The geometric and topological problem of which and how many possible types of architectures can be constructed by joining polyhedra was systematically addressed by A. F. Wells, who developed a comprehensive classification scheme.

From a theoretical point of view, many different types of structures are predictable, and it is also interesting to classify real structures based on this. However, the topological approach of arranging polyhedra in various ways does not take into account the bonding interactions between atoms/ions, somewhat like space groups that are not all equally frequent in crystal structures.

Furthermore, it must be clear that the description of crystal structures in terms of coordination polyhedron organization does not necessarily imply the actual existence of such species as separate and distinct entities. For example, we know well that sodium chloride, NaCl, is characterized by a primarily ionic bond, and thus there are no distinct octahedral entities of NaCl₆, just as we know that in the covalent crystal of silicon carbide, SiC, there are no separate tetrahedral entities of the type SiC₄. From a chemical standpoint, only in molecular crystals, such as in aluminum bromide, Al₂Br₆, can polyhedra be identified as distinct entities, or in species like silicates that contain groups of SiO₄ units.

Examples of Structures Based on Coordination Polyhedra

In sodium chloride, NaCl, each Na⁺ ion is surrounded by 6 chloride ions as first neighbors, arranged in a regular octahedron. We can schematically represent these NaCl₆ octahedra and consider how they are arranged and joined together to form the 3D structure. In this structure, each edge of the octahedra is shared with another octahedron, creating an infinite arrangement of octahedra exchanging all their edges.

In perovskite, CaTiO₃, the TiO₆ octahedra are connected by their vertices to form a 3D system of interconnected octahedra.

A similar arrangement is found in rhenium oxide, ReO₃.

There are several other examples of coordination polyhedron arrangements, many based mainly on tetrahedra and octahedra, which generate a wide variety of structures.

For example, sodium oxide NaO₂ with an antifluorite structure, from the perspective of coordination polyhedra, shows an arrangement of tetrahedra interconnected at the edges.

It is interesting, for instance, to observe the different spatial arrangements of tetrahedral coordination interconnected at the vertices in the two forms of zinc sulfide, Wurtzite (hcp) and Sphalerite (ccp).

Wurtzite

Sphalerite

Although completely different, a complete vertex interconnection of the tetrahedra is also found in quartz.

An interesting partial interconnection of the tetrahedra is found in cyclosilicates such as beryl Be₃Al₂(SiO₃)₆, which, in the presence of iron impurities, forms the precious gemstone "aquamarine".

An interesting layer-wise connection of tetrahedra is found in phyllosilicates such as micas, for example, in muscovite with the formula KAl₂(AlSi₃O₁₀)(OH)₂,

Organization of Coordination Polyhedra in Some Structures

With only Octahedra

12 shared edges	NaCl
6 shared vertices	ReO3
3 shared edges	CrCl3
2 shared edges and 6 vertices	TiO2
4 shared vertices	KAlF4

With only Tetrahedra

4 shared edges	NaO2
4 shared vertices	ZnS
4 shared vertices	SiO2
2 shared vertices	(SiO3)n2n-, chains or rings
1 shared vertex	Si2O76-