055PS - BASI STATISTICHE PER LA PSICOLOGIA 2022
Schema della sezione
-
Libro di testo adottato
Caudek, Luccio. 2001 Statistica per psicologi, collana Scienze della mente, editore Laterza. ISBN 9788842064190 (Capitoli 1-10)
Picconi. 2018 Elementi di Psicometria Vol 2. McGraw-Hill Education. ISBN: 9788838695261 (Supporto alla didattica ed esercizi)
Modalità di esame (2 esercizi "lunghi" da svolgere, tre definizioni teoriche con modalità di risposta aperta, due esercizi brevi).
Algebra introduttiva delle sommatorie.
Elementi di calcolo combinatorio; (Cap 1. Luccio e Caudek; Cap 3 Picconi).
-
Probabilità (Cap 1 Luccio & Caudek; Cap 2 Picconi)
Esercizi:
probabilità (Picconi pg 195 - 202).
-
Distribuzione di probabilità teorica (modello probabilistico) per una variabile aleatoria discreta
Valore atteso e sue proprietà
Convergenza con la media aritmetica in grandi campioni, sulla base della definizione frequentista di probabilità
Varianza, formula e proprietà.
(Cap. 3 Luccio e Caudek)
Esercizio:
Sistemate gli appunti usando un editor di testo (Word, ad esempio; selezionando Inserisci->Equazioni per attivare Equation Editor)
Calcolare il valore atteso e la varianza della variabile aleatoria discreta X che misura il numero di teste che si possono ottenere lanciando quattro monete oneste.
Verificate empiricamente le proprietà viste a lezione, scegliendo un valore arbitrario per "c" e duplicando la variabile aleatoria X in luogo di Y.
-
Lezione 3 File PDF
-
-
Variabile aleatoria definizione;
Istogramma: Rappresentazione grafica del modello probabilistico.
(Cap. 3 Luccio e Caudek)
-
La distribuzione di probabilità binomiale (Universi bernoulliani)
Valore atteso e varianza di una variabile aleatoria discreta binomiale.
Cap. 4 Luccio & Caudek
Cap 4 Picconi (4.1 -> 4.4 e schede di approfondimento)
Esercizi
1) Una confraternita ammette l'80 per cento dei richiedenti che soddisfano alcuni requisiti. Recentemente, quattro candidati appartaneneti ad una minoranza etnica hanno fatto domanda senza essere ammessi, nonostante soddisfacessero i requisiti. Calcolare la proabilità che nessuno di essi venga ammesso alla confraternita, se lo stesso criterio di ammissione viene applicato anche alla minoranza di cui fanno parte.
2) Una persona asserisce di essere in grado di indovinare molto spesso la faccia di una moneta (onesta) lanciata nell'altra stanza; di dieci lanci fatti ne indovina sette. Tirando ad indovinare, che probabilità avreste di fare altrettanto bene?
3) Una giuria (n = 12) viene scelta a caso da una lista di possibili candidati, dei quali il 53 per cento sono donne.
- Calcolare la probabilità che non venga scelta nessuna donna;
- che venga scelta una donna;
- determinare il valore atteso e la deviazione standard (radice quadrata della varianza) del numero di donne selezionate.
4) Un meteorologo asserisce che "la probabilità che piova di sabato è del 50 per cento, e che piova di Domenica ancora del 50 per cento. Quindi al 100 per cento pioverà in qualche giorno durante il fine settimana". Assumendo che la piovosità nelle due giornate sia indipendente, trovare la probablità corretta che piova almeno un giorno nel fine settimana.
5) Calcolare il valore atteso e la deviazione standard (radice quadrata della varianza) di- binomiale(n = 10; p = 0,50)
- binomiale(n = 10; p = 1/3)
- binomiale(n = 10; p = 2/3)
- Rappresentare graficamente le tre distribuzioni binomiali e confrontarle nei termini di Centro di Massa, Varianza e asimmetria.
6) Dal libro di Picconi, pg. 212 Es 1,3,4. (L'esercizio 2 ha soluzione sbagliata (p > 1), provate a risolverlo voi se volete, poi ne parliamo. Date un'occhiata alla corrigenda del libro di testo).-
BINOMIALE File PDF
-
La distribuzione normale.
La distribuzione normale standardizzata.
Standardizzazione dei punteggi (grezzi) di una variabile aleatoria gaussiana e soluzione di problemi sul calcolo delle aree sotto la curva normale standardizzata.
Cap. 4 Luccio & Caudek.
Cap. 4 Picconi (pg. 51-60)
1 Quale proporzione di casi in una distribuzione normale ricade nei seguenti intervalli:
- oltre un punto z pari a 2.10 (z > 2.10)
- prima di un punto z pari a -2.10 (z < -2.10)
- oltre un punto z pari a -2.10 (z > -2.10)
- tra gli z-score -2.10 e 2.10 (-2.10 < z < 2.10)
2 Mensa è una società di persone ad alto QI i cui membri hanno un punteggio al test QI pari o superiore al 98-esimo percentile.- Quante deviazioni standard oltre la media è posizionato il 98-esimo percentile?
- Per la distribuzione normale del QI con media 100 e deviazione standard 16, qual’è il punteggio del QI pari al 98-esimo percentile?
3 L’indice di sviluppo mentale infantile (MDI) è una misura standardizzata utilizzata in studi su bambini ad alto rischio. Questa variabile ha una distribuzione approssimativamente normale con media pari a 100 e deviazione standard pari a 16.- Definisci l’intervallo di valori MDI che contiene circa (i) il 68%, (ii) il 95% e (iii) tutte o quasi le osservazioni.
- Quale proporzione di bambini ha un valore MDI di almeno 120?
- Trova il punteggio di MDI pari al 90-esimo percentile.
- Trova il quartile inferiore, la mediana e il quartile superiore per MDI.
4 In occasione dell'esame intermedio per il corso di statistica, un esaminatore assegna sempre una valutazione pari a B agli studenti il cui punteggio è compreso tra 80 e 90. In un certo a.a., i punteggi hanno avuto una distribuzione normale con media pari a 83 e deviazione standard pari a 5. All'incirca, quale proporzione di studenti prenderà un voto B?
+ Esercizio 5 pg 212 (libro di Picconi)
-
GAUSS File PDF
- oltre un punto z pari a 2.10 (z > 2.10)
-
Misure di tendenza centrale, variabilità e forma di una distribuzione.
Trasformazione in punti z ed altre scale standardizzate (QI,Z,T,stanine, ecc.)
Cap. 5 Luccio & Caudek
Esercizi:- Dati is seguenti valori numerici arbitrari per le variabili X e Y:
X =(3,4,5,4,7,8)
Y =(3,4,5,4,19,21)
Calcolare media, deviazione standard, asimmmetria (G1), curtosi (g2) e trasformare i punti grezzi in punti z, verificando le proprietà 5.17 (media zero dei punti z) e 5.19 (varianze unitarie). - Anche mediante il foglio Excel allegato, svolgere l'esempio a pg.100-101 di Luccio.
-
Lezione 7 File XLSX
- Dati is seguenti valori numerici arbitrari per le variabili X e Y:
-
Cap.6 Luccio & Caudek (+ Cap 7 Luccio, Esempio 7.1 pg 115)
Proprietà della distribuzione campionaria della media.
Valore atteso, varianza e forma della distribuzione campionaria della media campionaria (Teorema del Limite Centrale).
Elementi essenziali mediante quattro simulazioni.-
Lezione 8 File PDF
-
-
Stima puntuale: proprietà degli stimatori
Cap.6 Luccio & Caudek-
Lezione 9 File PDF
-
-
Teorema centrale del limite:
approssimazione normale della distribuzione binomiale.
Paragrafo 7.3 Luccio pg. 120
Discussione esempio 7.1 Luccio pg. 115,
Discussione esempio 7.2 Luccio pg. 120.
-
Intervallo di fiducia per la media campionaria:
Cap.7 Luccio;
Esercizi.Ai partecipanti a uno studio è stato posto il seguente quesito: “Quale ritieni debba essere il numero ideale di figli per una famiglia?”La distribuzione delle risposte date dalle 497 donne intervistate presenta una media pari a 3.02. Ladeviazione standard della popolazione è conosciuta ed è pari a 1.81.- a) Riporta la stima puntuale della media della popolazione.
- b) Trova e interpreta l’errore standard della media campionaria.
- c) Trova l’intervallo di confidenza al 95%e interpretalo.
- d) Èplausibile che la popolazione abbia media = 2.0? Fornisci una spiegazione.
In riferimento all'esercizio precedente, per i 397 maschi del campione, la media era pari a 2.89 e la deviazione standard della popolazione era pari a 1.77.- a) Mostra che l’errore standard della media campionaria è 0.089.
- b) Troval’intervallo di confidenza al 95% per la media della popolazione e spiega cosa significa “fiducia al 95%”.
In uno studio si è chiesto ai partecipanti, “in quanti degli ultimi 7 giorni ti sei sentito triste?”Le risposte delle 816 donne hanno avuto media pari a 1.81. La deviazione standard della popolazione delle donne è pari a 1.98.Per i 633 intervistati maschi: media pari a 1.42. La deviazione standard della popolazione dei maschi è pari a 1.83.- a) Trova un intervallo di confidenza al 95% per la media della popolazione delle donne e degli uomini.
- b) Spiega perché i valori della media e della deviazione standard suggeriscono che questa variabile non ha una distribuzione normale. Ciò rappresenta un problema per il metodo dell’intervallo di confidenza determinato al punto a)? Fornisci una spiegazione.
PROBLEMA 1 (Approssimazione normale alla distribuzione binomiale)
In un sondaggio condotto negli USA, è stato chiesto agli intervistati se essi fossero favorevoli alle unioni civili. Dei 2003 adulti intervistati, il 54% ha detto SI, il 42% NO e il 4% non ha espresso opinioni.
Trova l’errore standard della stima per la proporzione campionaria di chi risponde SI. Fornisci un’interpretazione (definizione di errore standard di una statistica campionaria)
PROBLEMA 2 (Approssimazione normale alla distribuzione binomiale)
In un sondaggio condotto negli USA veniva posto agli intervistati il seguente quesito: “Ritieni che debba essere responsabilità del governo ridurre le differenze tra ricchi e poveri?”. Coloro che hanno risposto SI comprendevano 90 dei 142 soggetti che si autodefinivano “Democratici” e 26 dei 102 autodefinitisi “Repubblicani”.
a. Trova la stima puntuale della proporzione della popolazione che dovrebbe rispondere SI in ciascun gruppo;
b. Trova l’intervallo di confidenza al 95% per la proporzione della popolazione che risponde SI tra i Democratici;
c. Trova l’intervallo di confidenza al 99% per la proporzione della popolazione che risponde SI tra i Democratici;
d. Trova l’intervallo di confidenza al 95% per la proporzione della popolazione che risponde SI tra i Repubblicani;
e. Trova l’intervallo di confidenza al 99% per la proporzione della popolazione che risponde SI tra i Repubblicani;
f. Spiega come interpretare tali intervalli.
PROBLEMA 3 (Approssimazione normale alla distribuzione binomiale)
Un sondaggio negli USA ha chiesto se le attuali normative ambientali fossero troppo restrittive; dei 1200 rispondenti, 229 hanno detto che lo sono.
Trova e interpreta:
a. un intervallo di confidenza al 95% per il valore del parametro;
b. un intervallo di confidenza al 99% per il valore del parametro.
PROBLEMA 4
In un sondaggio è stato chiesto “Quale ritieni debba essere il numero ideale di figli per una famiglia?”. La distribuzione delle risposte delle donne intervistate (N = 497) presenta una mediana pari a 2, una media pari a 3.02 ed una deviazione standard pari a 1.81.
a. Riporta la stima puntuale della media della popolazione;
b. Trova e interpreta l’errore standard della media campionaria;
c. Trova l’intervallo di confidenza al 95% e fornisci un’interpretazione;
d. Trova l’intervallo di confidenza al 99% e fornisci un’interpretazione;
e. È plausibile che la popolazione abbia media=2.0? Fornisci una spiegazione.
PROBLEMA 5
In riferimento al problema precedente, per i 397 maschi del campione, la media era pari a 2.89 e la deviazione standard a 1.77.
a. Mostra che l’errore standard della media campionaria è 0.089;
b. Trova l’intervallo di confidenza al 95% per la media della popolazione e spiega cosa significa “fiducia al 95%”.
-
Intervallo di fiducia per la media campionaria:
discussione dell' esempio 6.1 a pg 112,
paragrafo 7.2 p. 116 - 119,
correzione di alcuni esercizi della lezione precedente.
-
Procedura di verifica di ipotesi statistiche.
Cap. 8 Luccio e Caudek (tranne 8.3 "indipendenza delle variabili").
Cap. 7 Picconi.
Esercizi: Dal libro di Luccio prestare attenzione all'esempio 7.1 pag. 115 prestare attenzione all'esempio 8.1 pag. 127 Da Picconi Esempio 7.1 pag. 134 Esempio 7.2 pag. 136 1-2-3-4-5
4pag. 229
pag. 231-
Lezioni 13 File PDF
-
-
Verifica di ipotesi e decisione: Errore di I e II tipo, potenza del test statistico
e discussione esempio 8.1 pp. 127 - 130 dal libro di Luccio.
-
Distribuzione Chi-quadrato ed intervalli di fiducia per la varianza della popolazione.
-
Lezione 15 File PDF
-
-
Verifica di ipotesi statistiche per il valore della varianza della popolazione, e per il confronto tra due varianze campionarie (distrubzione F)
Cap 8 Luccio
pg. 153 Picconi Paragrafo 8.4. La verifica delle ipotesi sulle varianze delle popolazioni
ATTENZIONE, nella consultazione dei valori critici F, le righe si riferiscono ai gradi di libertà associati alla varianza minore (DENOMINATORE per test su coda di destra) e le colonne ai gradi di libertà della varianza maggiore (NUMERATORE). Tale interpretazione vale sia per le tabelle in Luccio e Caudek che per il libro di Picconi.Esercizi per casa:
* Picconi. pg. 211 esercizio 3,4
** Picconi. pg. 241 esercizio 5
***Utilizzando la tabella delle aree del chi quadrato, individiare i valori corrispondenti ai seguenti casi.
- Coda di destra del 10%, con 7 gradi di libertà.
- Coda di sinistra del 2.5% con 9 gradi di libertà.
- 5% equamente divisi sulle code di destra e sinistra, con 10 gradi di libertà.
- 10% equamente divisi sulle code di destra e sinistra, con 20 gradi di libertà.
***Un campione casuale di 20 biglie in acciaio viene estratto da un processo produttivo il cui scostamento dal diametro atteso segue un andamento gaussiano. Le misure dei diametri ottenute sonox_1= {2.02, 1.94, 2.09, 1.95, 1.98, 2.00, 2.03, 2.04, 2.08, 2.07, 1.99, 1.96, 1.99, 1.95, 1.99, 1.99, 2.03, 2.05, 2.01, 2.03}
Considerando che il valore atteso (μ) e la varianza (σ2) dei diametri delle biglie del processo produttivo (gaussiano) sono entrambi ignoti,
- (a) Trovare un intervallo di fiducia al 95% per i parametri μ e σ2;
- (b) verificare l'ipotesi nulla μ = 2 (α = 0.05 e 0.025);
- (c) verificare se un nuovo campione casuale, x_2= { 1.97 1.98 1.85 1.90 1.94 2.02 1.97 1.96 1.83 2.04}, raccolto a distanza di un anno, consenta di non rifiutare un'ipotesi nulla che afferma NON esserci stato un deterioramento del processo produttivo, tale da causare un aumento della variabilità nei diametri delle biglie prodotte. (α = 0.05 e 0.025).
**** Mediante approssimazione normale alla distribuzione χ2 (vedi Luccio 9.1.3)
- si trovi il valore critico della coda destra della distribuzione chi-quadrato ponendo α = 0.05 e ν = 100
- si trovi il valore critico della coda destra della distribuzione chi-quadrato ponendo α = 0.025 e ν = 240
- si trovi il valore critico della coda sinistra della distribuzione chi-quadrato ponendo α = 0.025 e ν = 240
- si trovi il valore critico della coda sinistra della distribuzione chi-quadrato ponendo α = 0.250 e ν = 100
- si trovi il valore critico della coda destra della distribuzione chi-quadrato ponendo α = 0.100 e ν = 240
- si trovi il p-valore sulla coda di destra di χ2 = 123.2638 con ν = 100
- si trovi il p-valore sulla coda di sinistra di χ2 = 67.3800 con ν = 100
- si trovi il p-valore sulla coda di destra di χ2 = 261.1425 con ν = 240
-
Lezione 16 File PDF
-
Distribuzione t di Student.
t-test per una media campionaria
t-test per il confronto delle medie di due gruppi appaiati.
t-test e intervalli di fiducia per la differenza tra due medie campionarie.
----------------------------------------------------------------------------------------------
Cap 9 e 10 Luccio
Capitoli 8 e 10 dal libro di Picconi, più tutti gli esercizi degli stessi capitoli.
Picconi pag 99-102 (attenzione all'esempio 6.8, ma anche in quelli precedenti purtroppo, dove c'è un errore di stampa: la forma corretta è
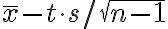. Vi ricordo che al denominatore dell'errore standard della media troviamo n-1 poichè la varianza campionaria utilizzata non è corretta per i gradi di libertà).Picconi pag. 132-140 e 229-238 (Esercizi...)
-
t-test per una media campionaria e per il confronto delle medie di due gruppi appaiati/indipendenti
ESERCIZI risolti in classe.
-
Verifica di ipotesi e intervallo di fiducia per la proporzione campionaria di successo.
Confronto tra due proporzioni campionarie di successo: Verifica di ipotesi e intervallo di fiducia per due campioni indipendenti.
esercizi:- Una ricerca condotta sul comportamento compulsivo negli acquisti ha realizzato alcune interviste telefoniche sul territorio nazionale USA su adulti di età uguale o superiore ai 18 anni. 44 su 800 uomini e 90 su 1501 donne sono stati giudicati come acquirenti incontrollabili secondo la “Compulsive Buying Scale”. a) Trova l’intervallo al 95% per la differenza tra le proporzioni di popolazione delle donne e degli uomini. b) Verifica, con α = 0.05, se le proporzioni di popolazione differiscono fra le donne e gli uomini.
- Per una verifica di Ho: π = 0.50, la proporzione campionaria è 0.35 secondo un campione di dimensione n=100. Calcolare la statistica test z; trova e interpreta il p-valore per Ha: π < 0.50; per un livello di significatività pari a 0.05, quale decisione puoi prendere? Se la decisione presa in c) fosse errata, di quale tipo di errore si tratterrebbe?
- In una elezione a sindaco vi sono due candidati; dato un campione casuale di 400 votanti, 230 hanno votato per un certo candidato. Sei disposto a prevedere il vincitore? perchè? Dato un campione casuale di 40 votanti, 23 hanno votato per un certo candidato. Sei disposto a prevedere il vincitore? perchè?
- Per un campione casuale di canadesi, il 60% dichiara di approvare l’operato del primo ministro. Una simile indagine un mese dopo ha una percentuale di favorevoli del 57%. a) Trova l’intervallo al 95% per la differenza tra le proporzioni. b) Verifica, con α = 0.05, se le proporzioni differiscono.
- Un sondaggio ha esaminato il consumo di alcool tra gli studenti del 2° anno di un’università francese. La percentuale di coloro che hanno dichiarato di bere alcolici più di 4 volte a settimana era pari a 39.9% di 12708 studenti nel 1997 e a 48.2% di 8783 studenti nel 2017. a) calcola l’errore standard per la stima della differenza tra le proporzioni nel 2017 e nel 1997 b) mostra l’intervallo di confidenza al 95% per la differenza.
-
La lezione di domani pomeriggio viene spostata a giovedì 22/12 con orario 9:00-12:00