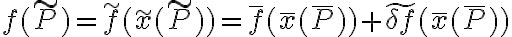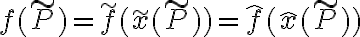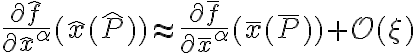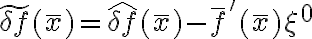Announcements

Carissimi,

nella derivazione di oggi della legge di trasformazione di una perturbazione 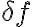$\delta f$ c'era qualche dettaglio che non tornava. La derivazione corretta è la seguente:

Sappiamo che per un punto fisico P vale 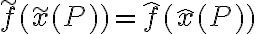$\tilde f (\tilde x(P)) = \hat f (\hat x(P))$, poiché f è scalare.

Le perturbazioni sono definite da

$f(\tilde P) = \tilde f (\tilde x (\tilde P)) = \bar f (\bar x (\bar P)) + \widetilde{\delta f} (\bar x (\bar P))$

$f(\hat P) = \hat f (\hat x (\hat P)) = \bar f (\bar x (\bar P)) + \widehat{\delta f} (\bar x (\bar P))$

da cui

$f(\tilde P) - f(\hat P) = \widetilde{\delta f} (\bar x (\bar P)) - \widehat{\delta f} (\bar x (\bar P))$.

Dalla natura scalare di f deriviamo

$f(\tilde P) = \tilde f(\tilde x (\tilde P)) = \hat f (\hat x(\tilde P))$

ora possiamo espandere l'ultima espressione attorno al punto di coordinate 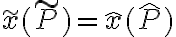$\tilde x(\tilde P) = \hat x(\hat P)$ usando $\hat x(\tilde P) = \tilde x (\tilde P) - \xi$:

$f(\tilde P) = \hat f (\tilde x(\tilde P) - \xi(\bar P) ) = \hat f (\hat x(\hat P) - \xi(\bar P) ) \approx \hat f (\hat x(\hat P)) - \frac{\partial\hat f}{\partial \hat x^\alpha} \xi^\alpha$

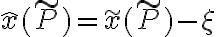La derivata possiamo approssimarla come

$\frac{\partial\hat f}{\partial \hat x^\alpha}(\hat x(\hat P)) \approx \frac{\partial\bar f}{\partial \bar x^\alpha} (\bar x (\bar P)) + \mathcal O (\xi)$

ottenendo

$f(\tilde P) = f(\hat P) - \frac{\partial\bar f}{\partial \bar x^\alpha} \xi^\alpha = f(\hat P) - \frac{\partial\bar f}{\partial \bar \tau} \xi^0$.

Il risultato finale è quindi

$\widetilde{\delta f} (\bar x) = \widehat{\delta f} (\bar x) - \bar f'(\bar x) \xi^0$

A lezione ho scritto l'ultima equazione col segno 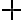$+$ anziché $-$, è un errore.