Schema della sezione

  • Distribuzione t di Student.

    t-test per una media campionaria e per il confronto delle medie di due gruppi appaiati.

    Test e intervalli di fiducia per la differenza tra due medie campionarie.

    .................................

    Cap 9 e 10 Luccio

    Capitoli 8 e 10 dal libro di Picconi, più tutti gli esercizi degli stessi capitoli.

    Picconi pag 99-102 (attenzione all'esempio 6.8, ma anche in quelli precedenti purtroppo, dove c'è un errore di stampa: la forma corretta è 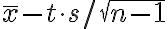\bar{x} -t\cdot s/\sqrt{n-1} . Vi ricordo che al denominatore dell'errore standard della media troviamo n-1 poichè la varianza campionaria utilizzata non è corretta per i gradi di libertà).

    Picconi pag. 132-140 e 229-238 (Esercizi...)


    Registrazione di Microsoft Teams (22 Dicembre 2021)
    https://units.sharepoint.com/:v:/r/sites/PATC_CD2021_PS01_055PS_289454/Documenti%20condivisi/General/Recordings/Solo%20visualizzazione/Meeting%20in%20_General_-20211222_093430-Meeting%20Recording.mp4?csf=1&web=1&e=gWBw2O

    ....................................................



    Esercizio 1

    Secondo un accordo sindacale, il reddito medio dei lavoratori senior nell'azienda XY deve essere pari a $ 500 a settimana. Si decide di analizzare se il reddito medio µ delle lavoratrici donne è conforme all'accordo. Per un campione casuale di nove donne occupate sono stati ottenuti i valori, ȳ = $ 410, s = $ 90.


    • verifica se il reddito medio delle donne lavoratrici è differente da $ 500 alla settimana. Esplicita le assunzioni, le ipotesi, il test e il p-valore. Interpreta il risultato
    • riporta e interpreta il p-valore per Ha: µ < 500
    • riporta e interpreta il p-valore per Ha: µ > 500

    Esercizio 2

    A n = 10 studenti universitari è stato chiesto di stabilire quante volte al mese nell’anno precedente avevano preso parte alle seguenti attività: andare al cinema e andare ad un evento sportivo. I dati ottenuti sono riportati nella tabella sotto. Calcolare la statistica test t e riportare le conclusioni per l’ipotesi nulla ( \alpha=0.05 ).




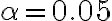    Esercizio 3
    I risultati di una ricerca che ha confrontato maschi e femmine rispetto al numero di numero di ore al giorno in cui il soggetto guarda la tv sono stati:
    Gruppo F: N=1117, Media=2.99, dev. stan.=2.34
    Gruppo M: N=870, Media=2.86, dev.stan.=2.22
    a)conduci un test di significatività per analizzare se le medie di popolazione differiscono tra i maschi e le femmine. Riporta le conclusioni per il livello di significatività ɑ=0.05 b)un intervallo di confidenza al 95% per il confronto di medie conterrebbe lo 0?
    c)pensi che la distribuzione delle ore dedicate a guardare la tv sia approssimativamente normale? la risposta a questa domanda ha qualche implicazione per le conclusioni tratte nel punto (a)?

    Esercizio 4
    Nella tabella sono riportati i dati ottenuti confrontando due gruppi di partecipanti di età 21-30 e 31-40 rispetto al numero di numero di ore al giorno in cui i partecipanti usano il cellulare:

    Gruppo  N
    		 Media
    		 s
     21-30

     31-40     		1200

    945     		  4.20

      3.40    		 1.60

    2.40

    a)costruisci l’intervallo di confidenza al 95% per il confronto di medie; cosa puoi dedurre?
    b)conduci un test di significatività per analizzare se le medie di popolazione differiscono tra i partecipanti di età 21-30 e 31-40. Riporta le conclusioni per il livello di significatività ɑ=0.05