4 Lezione
Schema della sezione
-
Giovedì 05 ottobre -2023
h 16:30 - 19:00
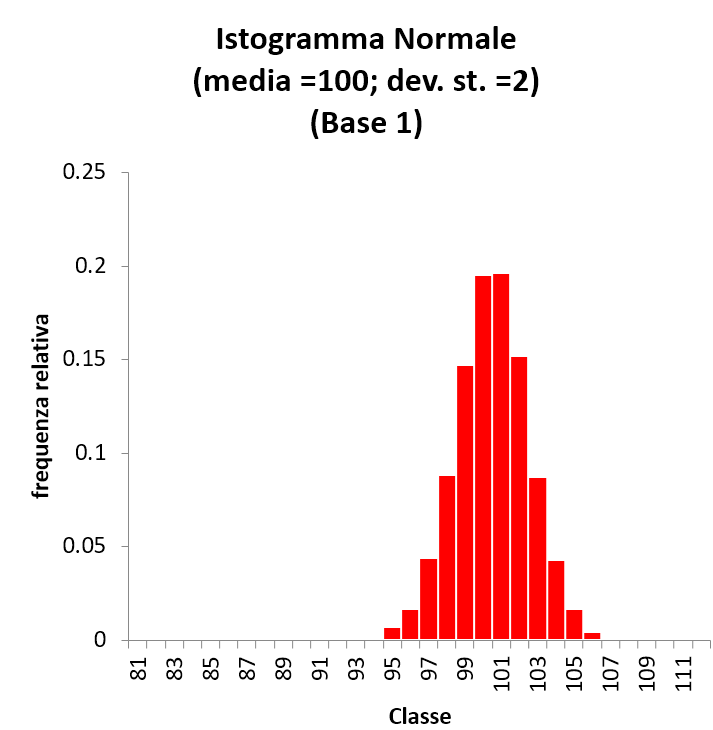
Istogramma: Rappresentazione grafica del modello probabilistico.
Applicazione pratica con Excel.
(Cap. 3 Luccio e Caudek)
Esercizio:- Mediante applicativo Excel, randomizzare 10000 valori "Normali" come media = 10 e dev. st = 1. (Le figure e il foglio Excel riportano invece dati simulati con mu =100 e sd =2)
- Calcolare il valore minimo e massimo dei valori ottenuti
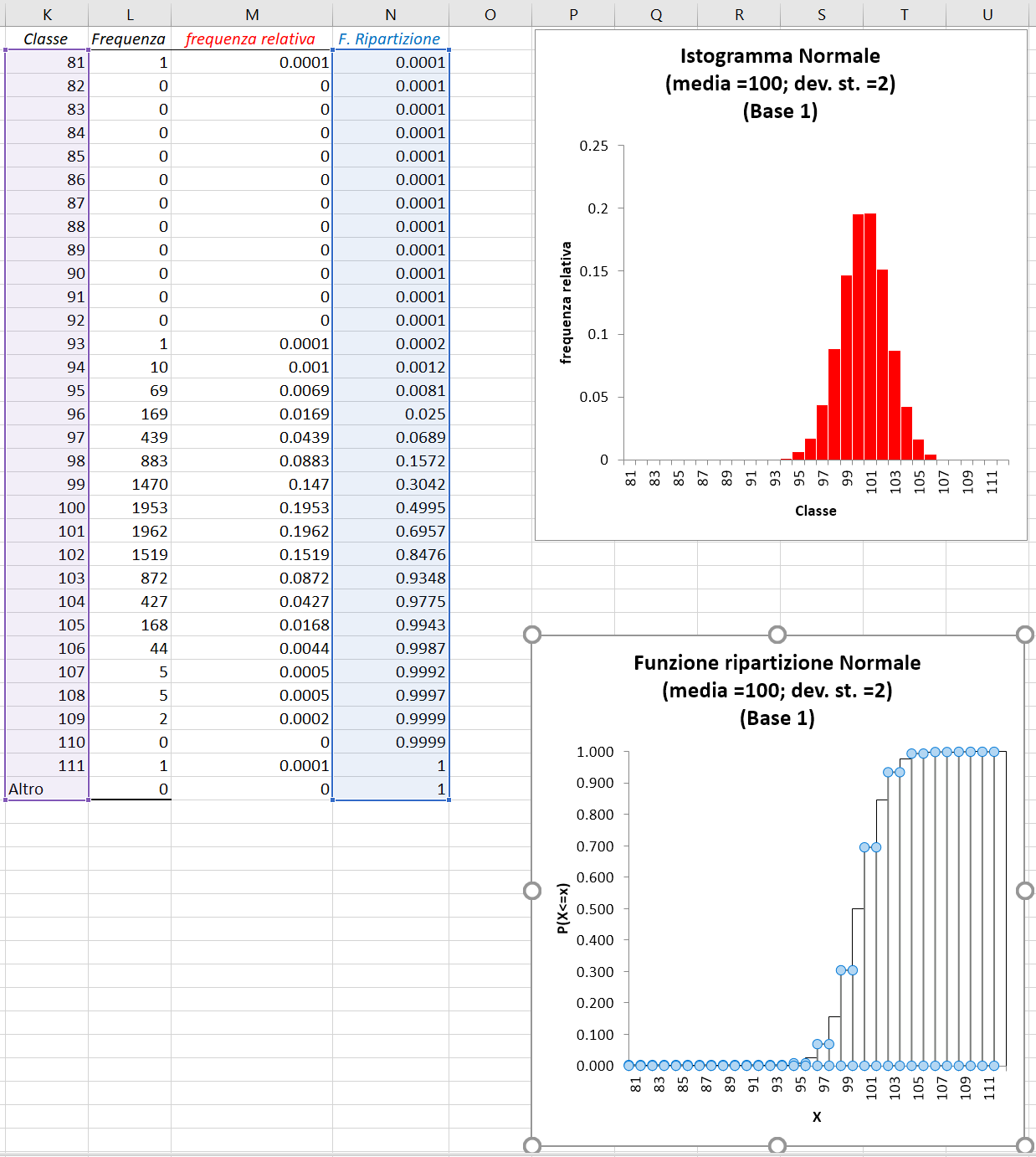
- Impostando il valore minimo, creare una sequenza di base = 1 fino al valore massimo.
- Utilizzare la sequenza come "intervallo di classe" per generare l'istogramma.
- Calcolare la colonna "frequenza relativa" e modificare l'asse y dell'istogramma ottenuto (che sarà così di Area = 1)
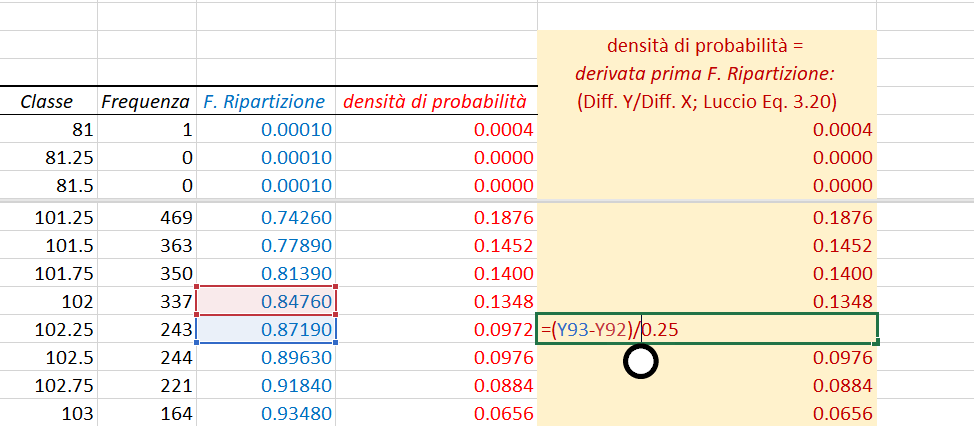
- Calcolare la colonna "Funzione di ripartizione"
- Copiare e incollare il grafico dell'istogramma, selezionando come valori in ordinata la colonna "Funzione di ripartizione", generando il grafico cumulativo "a scalini".
----------------------------------------------------------------------------------------- Impostando il valore minimo, creare una sequenza di base = 0.25 fino al valore massimo.
- Utilizzare la sequenza come "intervallo di classe" per generare un nuovo istogramma.
- Calcolare la colonna "densità di probabilità" (freq. relativa/0.25) e modificare l'asse y dell'istogramma ottenuto (che sarà così di Area = 1)
- Calcolare la colonna "Funzione di ripartizione"
- Copiare e incollare il grafico dell'istogramma, selezionando come valori in ordinata la colonna "Funzione di ripartizione", generando il grafico cumulativo.
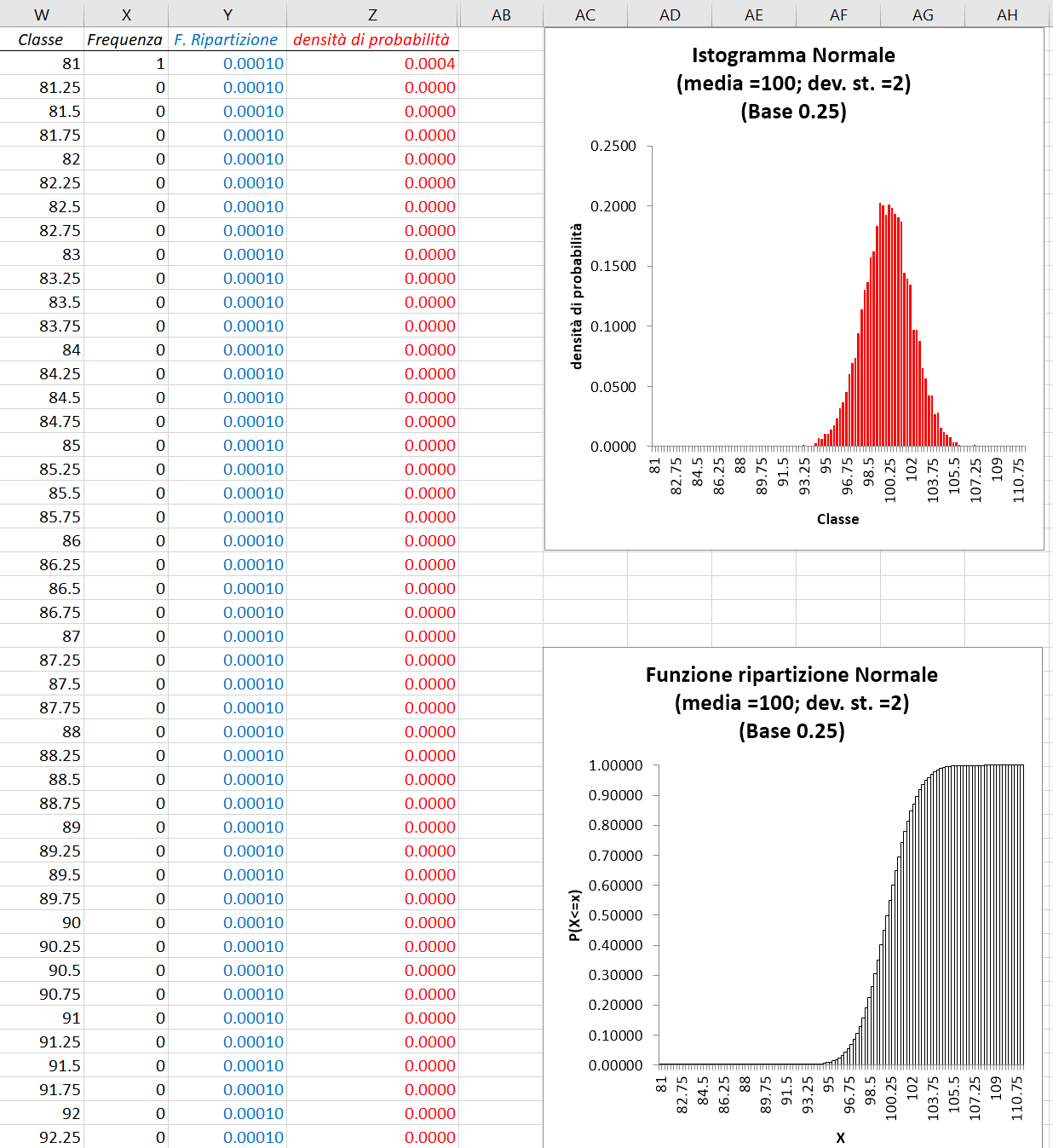
- Osservare come, disponendo di un grande numero di osservazioni di una variabile aleatoria continua, riducendo l'ampiezza delle classi (basi dei rettangolini che costituiscon l'istogramma), aggiustando l'unità di misura lungo l'asse delle ordinate (densità di probabilità = freq. relativa classe/ampiezza classe; ->area rettangolo= freq. relativa; --> area tot= 1), allora l'istogramma e la funzione di ripartizione somiglieranno ad una funzione continua che ne interpola il profilo discontinuo.
- Verificare (Luccio, eq. 3.20) che la funzione di densità di probabilità di una variabile aleatoria continua, può essere definita come "derivata prima della funzione di ripartizione".