Schema della sezione

  • Lunedì 30 ottobre 2023

    h 16:30 - 18:00

    Teorema centrale del limite: 

    approssimazione normale della distribuzione binomiale. 

    Paragrafo 7.3 Luccio (pg. 120)

    Discussione esempio 7.1 Luccio (pg. 115),

    Discussione esempio 7.2 Luccio (pg. 120).

    Domande ed esercizi di ripasso Lezioni 10/11:
    1) Enunciare il Teorema del Limite Centrale.
    2) Definire distribuzione campionaria di una statistica.
    3) Relativamente alle proprietà di uno stimatore puntuale, cosa si intende per Correttezza, Efficienza e Consistenza?
    4) Cosa si intende per approssimazione normale alla distribuzione binomiale?
    5) Quale stimatore puntuale del centro di una distribuzione Gaussiana è più efficiente tra Media e Mediana (Perché?)
    6) Cosa indica il concetto di correzione (di una statistica) per i suoi gradi di libertà?
    7) A cosa è uguale la seguente quantità? (Anche mediante dimostrazione) 

    E\left(\sum{ \frac{(x_i-\bar{x})^2}{n} } \right)=?

    8) Cosa si intende per Errore Standard di una statistica campionaria?

    9) Quanto valgono valore atteso e varianza della distribuzione campionaria della media calcolata su n = 100 soggetti, sapendo che i dati sono tratti da una popolazione con 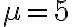 \mu = 5 e  \sigma^2 = 36 ?

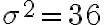    10) Dato un generico indice statistico corretto 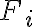F_i , la cui distribuzione campionaria non è nota, che probabilità c'è che il valore ottenuto non ecceda due deviazioni standard di distanza dal parametro ignoto  \phi ?

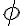    11) Mediante approssimazione normale alla binomiale, completare la distribuzione di probabilità di k successi in n=7 prove indipendenti di Bernoulli ( p=0.50 ).

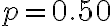    12) Calcolare la probabilità di k = 7 successi in n = 30 prove indipendenti di Bernoulli, con 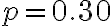p=0.30. Stimare la stessa probabilità mediante l'approssimazione normale.