114SM - MATEMATICHE COMPLEMENTARI 2018/19
Schema della sezione
-
-
L'esame è costituito da una prova scritta e da un colloquio orale. La prova scritta è costituita dalla risoluzione di due esercizi. La prova orale consiste di quesiti sulla teoria svolta ed eventuali esercizi. Durante il corso vengono assegnati degli esercizi per casa in preparazione alla prova scritta.
-
-
Testo molto ricco e interessante, da consultare, non da studiare sistematicamente.
-
-
5/09/18. Equazione di d'Alembert, costruzione sommaria del modello della corda vibrante. Formula di Vincenzo Galilei. Soluzioni a variabili separate. Modo principale, frequenza principale. Soluzione di d'Alembert dell'equazione della corda vibrante. Legge di Mersenne.
-
10/10. Corda pizzicata. Traccia della derivazione dell'equazione del calore.12/10. Soluzioni a variabili separate dell'equazione del calore. Serie di Fourier, coefficienti di Fourier, nucleo di Dirichlet. Lemma di Riemann-Lebesgue. Un criterio di convergenza puntuale per le serie di Fourier.
-
17/10. Convergenza in un punto di discontinuità di prima specie. Una rappresentazione del nucleo di Dirichlet. Medie di Cesàro, teorema di Fejer e sue conseguenze.Teorema di Lebesgue sull'integrabilità secondo Riemann (solo enunciato)19/10. Richiamo sulla disuguaglianza di Schwarz. Disuguaglianza di Bessel. Coefficienti di Fourier della derivata. Un criterio di convergenza uniforme per le serie di Fourier. Richiai sui numeri complessi, serie di potenze, funzione esponenziale:
-
24/10. Serie di Fourier in termini di esponenziali immaginari. Serie di soli coseni e di soli seni. Cambio di scala nelle serie di Fourier. Esercizi
-
-
31/10. Richiami su spazi con prodotto scalare, disug. di Schwarz, identità del parallelogramma. Spazi di Hilbert. Teorema di proiezione su un convesso.Teorema di proiezione ortogonale. Sistemi ortonormali. Disuguaglianza di Bessel.
02/11. Sospensione delle lezioni del CdL.
-
07/11.Sistemi ortonormali completi e caratterizzazioni equivalenti. Convergenza in norma 2 delle serie di Fourier trigonometriche. Disuguaglianza di Wirtinger. Teorema isoperimetrico.
09/11. Principio di massimo per l'equazione del calore, risoluzione dell'equazione del calore ( v. appunti qui sotto). Equazione di Laplace e principio di massimo per funzioni armoniche. Problema di Dirichlet in un rettangolo.
-
-
14/11. Problema di Dirichlet nel disco, nucleo di Poisson. Convergenza alla Abel delle serie di Fourier.
16/11. Soluzioni dell'equazione del calore periodiche nel tempo, e la cantina di Fourier. Problema di Dirichlet nella corona circolare.
-
21/11. Serie di Fourier multiple, un criterio per la convergenza uniforme. Trasformata di Fourier. Spazio di Schwarz, Gaussiana. Prime proprietà della trasformata.
23/11. Formula di moltiplicazione. Teorema di inversione. Identità di Plancherel. Trasformata di Fourier su
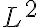(cenni). Trasformata di Fourier in più variabili, proprietà di base. -
28/11. Equazione del calore su
. Nucleo del calore. Esistenza e unicità per il problema ai valori iniziali.30/11. Principio di indeterminazione di Heisenberg. Teorema di campionamento di Shannon.
-
05/12. Teorema di somma di Poisson. Nucleo di Poisson del semipiano. Teorema di Carleson (solo enunciato).
07/12. Lezione sospesa.
-
scritti MC File RAR
-
-
12/12. Esercizi.
14/12. Esercizi.