113SM-1 - ISTITUZIONI DI ANALISI E GEOMETRIA - MODULO A 2018/19
Schema della sezione
-
-
L'esame è costituito da una prova scritta e da un colloquio orale. La prova scritta è costituita dalla risoluzione di tre esercizi. La prova orale consiste di quesiti sulla teoria svolta ed eventuali esercizi. Durante il corso vengono assegnati degli esercizi per casa in preparazione alla prova scritta.
-
04/10. Lezione sospesa per indisposizione del docente. Prima lezione spostata al giorno 8/10.
-
09/10. Algebre, sigma-algebre, misure.11/10. Massimo e minimo limite di insiemi. Misure finite, sigma-finite, complete. Teorema di completamento. Misura esterna.
-
15/10. Intervalli in
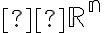 , misura
esterna di Lebesgue, sigma-algebra e misura di Lebesgue. Misurabilità
dei semispazi. Teorema di ricoprimento di Whitney. I
Boreliani sono insiemi di Lebesgue.
, misura
esterna di Lebesgue, sigma-algebra e misura di Lebesgue. Misurabilità
dei semispazi. Teorema di ricoprimento di Whitney. I
Boreliani sono insiemi di Lebesgue.18/10. Misura degli intervalli. Caratterizzazione per approssimazione degli insiemi di Lebesgue, inizio della dimostrazione.
-
22/10. Caratterizzazione per approssimazione degli insiemi di Lebesgue, fine della dimostrazione. Insieme di Vitali. Misura su un'algebra.25/10.Teorema di estensione di Caratheodory. Nozione di misura esterna regolare. Esercizi.
-
1,2/11. Lezioni sospese per tutto il C.d.L.
29/10. Misura su una semialgebra.
-
05/11. Esercizi. Funzioni misurabili.06/11. Operazioni su funzioni misurabili. Successioni di funzioni misurabili. Convergenza quasi ovunque. Approssimazione di funzioni misurabili con funzioni semplici.
-
12/11.Convergenza quasi uniforme. Teorema di Egorov-Severini. Convergenza in misura, convergenza alla Cauchy in misura. Esempi. Convergenza alla Cauchy in misura e convergenza q.uniforme di una sottosuccessione. Funzioni misurabili su
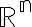 e approssimazione in misura con funzioni a scalino.
e approssimazione in misura con funzioni a scalino.15/11. Funzioni misurabili su
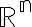 e approssimazione in misura con funzioni
continue. Teorema di Tietze (solo enunciato). Teorema di Lusin. Esercizi.
e approssimazione in misura con funzioni
continue. Teorema di Tietze (solo enunciato). Teorema di Lusin. Esercizi.
-
19/11. Integrale di funzioni misurabili nonnegative. Lemma di Fatou. Teorema di convergenza monotona. Conseguenze del Teorema di convergenza monotona. Integrale per funzioni di segno variabile.22/11.Teorema di convergenza dominata. Varianti ai teoremi di passaggio al limite sotto il segno di integrale. Teorema di derivazione sotto il segno di integrale (cenni). Proprietà dell'integrale.
-
26/11. Confronto tra integrale di Riemann e di Lebesgue. Integrale improprio e integrale secondo Lebesgue. Criterio di Lebesgue per l'integrabilità secondo Riemann (cenno). Misure prodotto.23/11. Principio di Cavalieri. Teorema di Fubini.Teorema di Tonelli e conseguenze, funzione distribuzione. Misura prodotto su
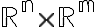 .
.
-
Per "riscaldamento".
-
-
spaziLp File PDF
-
-
10/12. Disuguaglianza di Minkowski integrale. Proprietà di monotonia della norma
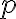 , disuguaglianza interpolatoria, limite della norma
, disuguaglianza interpolatoria, limite della norma 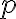 per
per 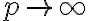 .13/12. Approssimazione in
.13/12. Approssimazione in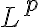 con funzioni semplici, e a scalino.
Continuità nel senso di
con funzioni semplici, e a scalino.
Continuità nel senso di 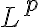 . Disuguaglianza di Young per
convoluzioni, un caso particolare. Nuclei
mollificatori. Approssimazioni di funzioni
. Disuguaglianza di Young per
convoluzioni, un caso particolare. Nuclei
mollificatori. Approssimazioni di funzioni 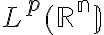 con
funzioni
con
funzioni 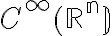 e con funzioni
e con funzioni
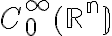 .
.
-
-
07/01. Esercizi.10/01. Esercizi.
-
IAGA4lug16 File PDF
-
solIAGA4lu File PDF
-
soluzioni File PDF
-
IAGA13giu19 File PDF
-
Scritto del 24/9: nessun ammesso.
-
IAGA2lug19 File PDF
-
IAGA 2 LUG File PDF
-